Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A Locality Repair Coding Method Based on Pyramid Codes

A technology of partial repair and encoding method, applied in the computer field, can solve the problem of high disk I/O overhead, achieve the effect of small repair bandwidth overhead and ensure storage overhead

Inactive Publication Date: 2019-08-02
CHANGAN UNIV
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0003] In the cloud storage system, there is a high probability that two or more nodes will fail at the same time. The existing SRC and LRC have good repair locality when repairing a node failure, but when repairing two or more failed nodes, it needs Connecting multiple surviving nodes, the disk I / O overhead is high

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Locality Repair Coding Method Based on Pyramid Codes
  • A Locality Repair Coding Method Based on Pyramid Codes
  • A Locality Repair Coding Method Based on Pyramid Codes

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0035] Such as Figure 1-3 As shown, in accordance with the above technical solution, this embodiment provides a localized repair coding method based on Pyramid codes. The minimum coding structure of Pyramid codes refers to the ability to quickly repair the Pyramid code coding method and ensure that the least number of nodes participate in the repair process.

[0036] It mainly includes the following steps: there are many storage nodes in the distributed storage system, assuming that there are n storage nodes in the distributed storage system, each storage node stores a data block, and every 8 storage nodes are regarded as a minimum coding structure C, where C=D·G, D=[d 11 , d 12 ,...,d ij ,...,d tj ], d ij j data blocks stored for the i-th partial repair group, i represents the i-th partial repair group, i≤t, j represents the number of data blocks stored in the local repair group, 1≤j≤4 and is an integer; there are t local repair groups, G=[I|P] represents the generation...

Embodiment 2

[0044] This embodiment provides a storage node failure recovery method in a distributed storage system, including the following steps:

[0045] Step 1: Encoding all n storage nodes in the distributed storage system by using the local repair encoding method described in Embodiment 1;

[0046] Step 2, storage node failure repair;

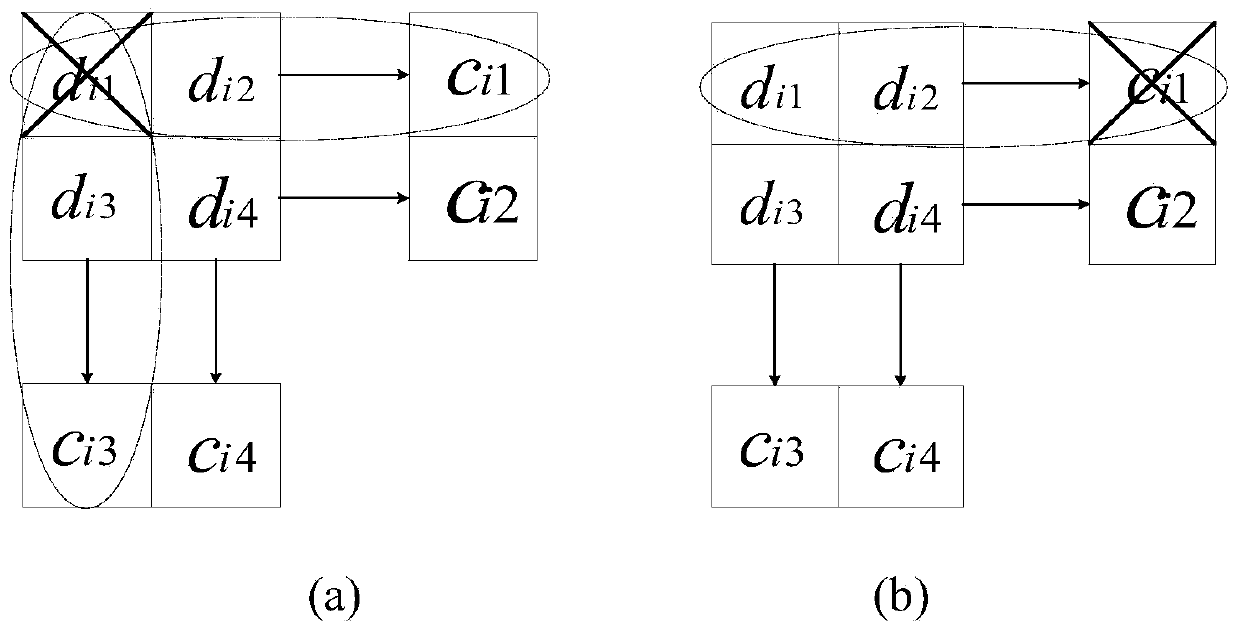
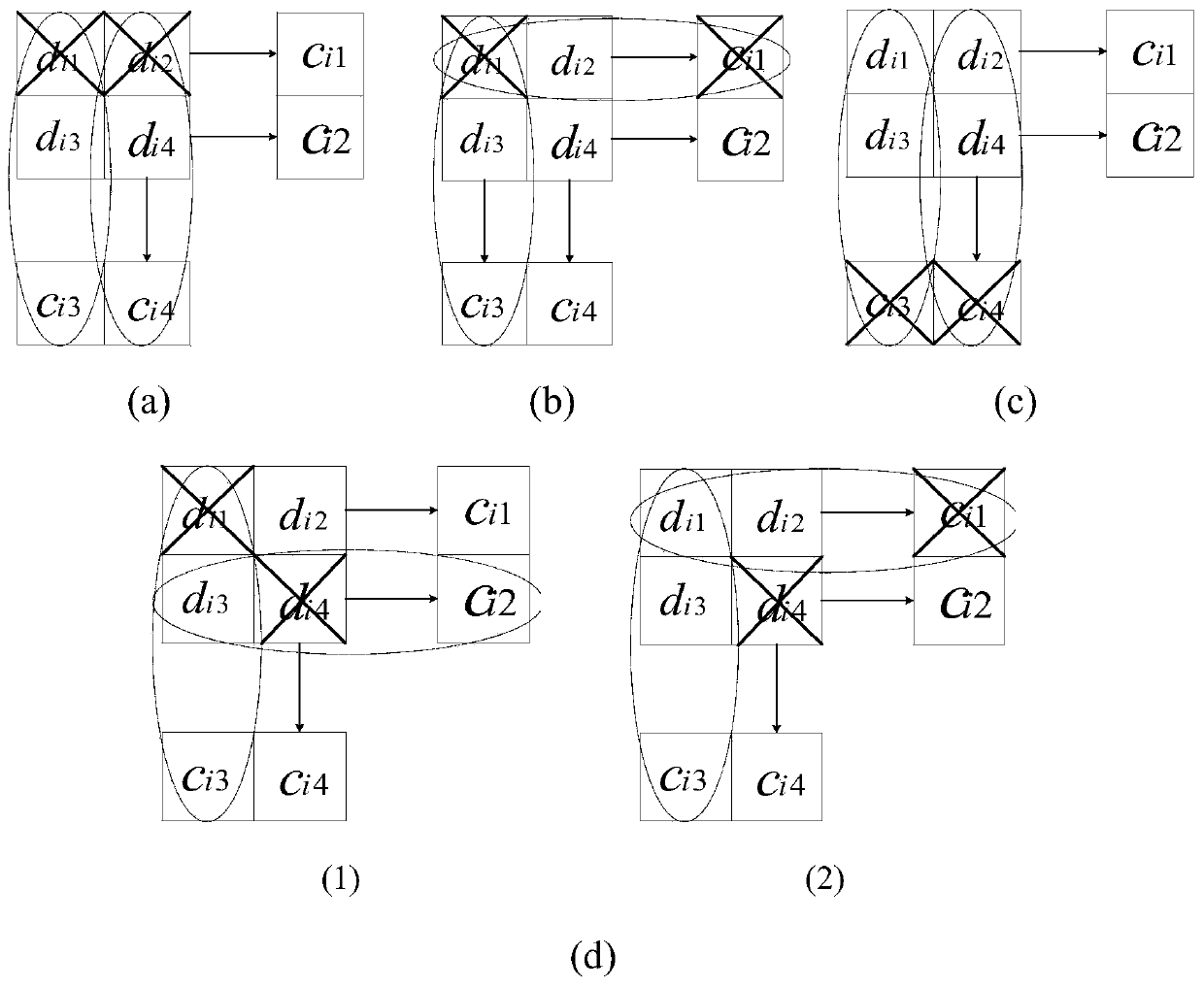
[0047] Assume that in the i-th local repair group of t local repair groups, there is a storage node failure, and the non-failure storage node is a surviving storage node; the i-th local repair group contains four data blocks d i1 、d i2 、d i3 and d i4 and four check blocks c i1 、c i2 、c i3 and c i4 , where d i1 、d i2 、d i3 and d i4 It is a data block arranged in two rows and two columns, c i1 for d i1 and d i2 Generated by linear encoding of the generator matrix G, c i2 for d i3 and d i4 Generated by linear encoding of the generator matrix G, c i3 for d i1 and d i3 Generated by linear encoding of the generator matrix G, c i4 for d ...

Embodiment 3

[0056] Such as Figure 4 , the present embodiment assumes that there are 8 storage nodes in the distributed storage system, and the Pyramid code is constructed in a storage structure in which the minimum coding structure is 8 storage nodes, and D=[d 1 , d 2 , d 3 , d 4 ] represents the data block stored by the storage node in the minimum coding structure, where d 1 , d 2 , d 3 , d 4 respectively represent the information of a single data block; G=[I|P] represents the generator matrix required to generate the coded data block C, where I is the identity matrix and P is the 4×4 sub-matrix. Then C is recorded as: C=[d 1 , d 2 , d 3 , d 4 ,c 1 ,c 2 ,c 3 ,c 4 ],

[0057] Generate matrix here

[0058]

[0059] where the variable g 12 , g 13 , g 21 , g 24 , g 31 , g 34 , g 42 and g 43 Indicates the coding coefficient of the Pyramid code. The expression of the check block can be known from the generator matrix, c 1 =g 12 d 1 +g 21 d 2 , c 2 =g 34 d 3...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a locally repairing and coding method based on a Pyramid code. A minimum code structure C of the Pyramid code serves as a basic code structure, and storage nodes of a distributed type storage system are grouped according to the number of the storage nodes required by the minimum code structure of the Pyramid code. At the same time, the invention further discloses a method for repairing failure storage nodes by means of the locally repairing and coding method based on the Pyramid code. In a Pyramid-code-based locally repairing and coding structure constructed by means of the method, all of verifying blocks of the storage nodes in locally repairing groups are generated by locally coding of data blocks stored in the locally repairing groups, based on the coding structure, when single-node faults and two-node faults exist in the locally repairing groups, it is only required to connect limited survival nodes in the locally repairing groups to quickly achieve data reconstruction of the failure nodes in the locally repairing groups, and failure storage node data is restored.

Description

technical field [0001] The invention belongs to the field of computers and relates to a Pyramid code-based local repair coding method. Background technique [0002] Current distributed storage systems usually use erasure codes to improve storage reliability, among which Maximum Distance Separable (MDS) codes can improve system storage efficiency while ensuring system reliability. However, erasure coding needs to download the data volume of the entire file size when repairing the faulty node, and the repair bandwidth overhead is too large. In order to reduce the repair bandwidth overhead of traditional erasure codes, Dimakis et al. proposed regeneration codes, which significantly reduced the repair bandwidth overhead of faulty nodes. By analyzing the repair bandwidth and storage overhead, Dimakis et al. proposed a minimum storage regeneration (Minimum Storage Regeneration, MSR) code and a minimum bandwidth regeneration (Minimum Bandwidth Regeneration, MBR) code in 2010. Sim...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F11/10H04L29/08
CPCG06F11/1076H04L67/1097
Inventor 王静张崇杨洋
Owner CHANGAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com