Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

A hyperspectral image unmixing method based on endmember-constrained non-negative matrix factorization

A non-negative matrix decomposition and hyperspectral image technology, which is applied in image analysis, image enhancement, image data processing, etc., can solve the problems that affect the optimal solution acquisition and the existence of local minima, so as to improve the unmixing accuracy and slow down the The effect of mutation

Inactive Publication Date: 2019-05-21
HEILONGJIANG UNIVERSITY OF SCIENCE AND TECHNOLOGY
View PDF2 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

The objective function of the classic NMF algorithm has obvious non-convexity, and there are local minimum values, which affect the optimal solution

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A hyperspectral image unmixing method based on endmember-constrained non-negative matrix factorization
  • A hyperspectral image unmixing method based on endmember-constrained non-negative matrix factorization
  • A hyperspectral image unmixing method based on endmember-constrained non-negative matrix factorization

Examples

Experimental program
Comparison scheme
Effect test

specific Embodiment approach 1

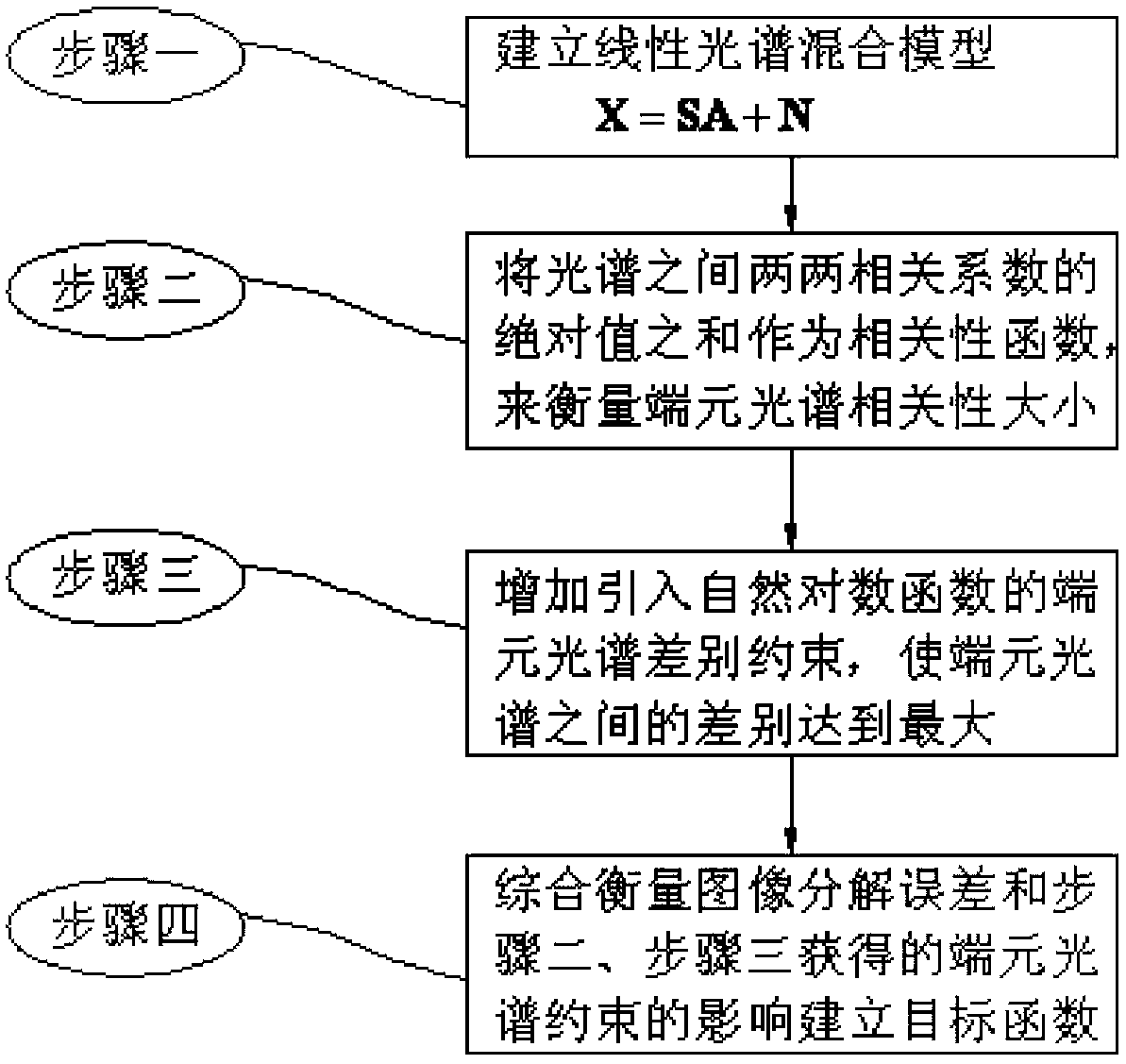
[0019] The hyperspectral image unmixing method based on endmember constrained non-negative matrix decomposition of this embodiment, combined with figure 1 As shown, the method is realized through the following steps:

[0020] Step 1. Set the pixel spectral vector X, the endmember spectral matrix S, the abundance matrix A of the N-dimensional vector, and the random noise N to establish a linear spectral mixing model:

[0021] X=SA+N (1)

[0022] Wherein, the endmembers refer to various substances contained in the pixels of the hyperspectral image presented by the spectral imager, and these pixels containing the endmembers are called mixed pixels;

[0023] Step 2, using the sum of the absolute values ​​of the pairwise correlation coefficients between the spectra as a correlation function to measure the size of the endmember spectral correlation;

[0024] Step 3, adding the endmember spectrum difference constraint introduced by the natural logarithm function, so that the differ...

specific Embodiment approach 2

[0026] The difference from Embodiment 1 is that in the hyperspectral image unmixing method based on endmember-constrained non-negative matrix decomposition in this embodiment, in the linear spectral mixing model X=SA+N described in step 1, the endmember spectral matrix S= [s 1 ,s 2 ,...,s N ], the element s in the endmember spectral matrix S i Represents the endmember vector, i∈[1,N]; the abundance matrix A of N-dimensional vector=[a 1 ,a 2 ,...,a N ] T , each component element in the abundance matrix A of the N-dimensional vector represents the abundance of the corresponding end member, and

[0027] a i ≥0 (2)

[0028]

[0029] Wherein, the abundance refers to the proportion of one type of end member in the pixel.

specific Embodiment approach 3

[0030] The difference from the specific embodiment 1 or 2 is that in the hyperspectral image unmixing method based on endmember constrained non-negative matrix decomposition in this embodiment, as described in step 2, the sum of the absolute values ​​of the pairwise correlation coefficients between the spectra is used as the correlation The process of measuring the magnitude of the endmember spectral correlation is,

[0031] Step 21. Perform non-negative matrix decomposition based on endmember constraints:

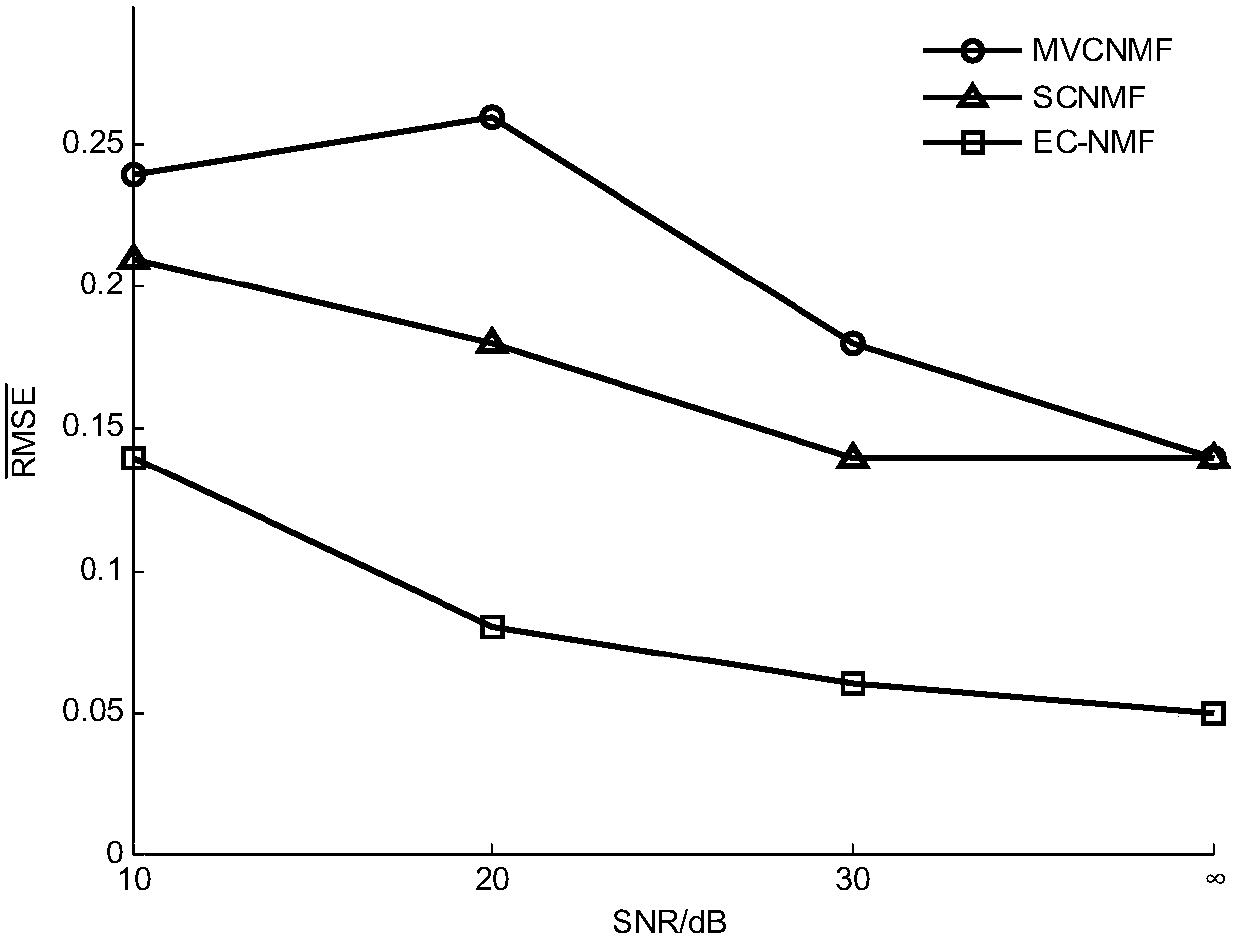
[0032] Using the NMF algorithm, by minimizing the Euclidean distance objective function, the optimal solution of S and A is obtained when X is known.

[0033]

[0034] The iteration formula is:

[0035] S←S-β 1 (SA-X)A T (5)

[0036] A←A-β 2 S T (SA-X) (6)

[0037] The NMF-based spectral unmixing algorithm does not need to determine whether there is a pure pixel, and obtains the abundance of the corresponding endmember while extracting the endmember;

[0038] I...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a hyperspectral image unmixing method based on endmember constrained non-negative matrix decomposition, which belongs to the field of hyperspectral image decomposition methods. The objective function of classical non-negative matrix factorization is non-convex, which affects the optimal solution. A hyperspectral image unmixing method based on endmember-constrained non-negative matrix factorization, which uses the sum of the absolute values ​​of pairwise correlation coefficients between spectra as a correlation function to measure the magnitude of endmember spectral correlation. The natural logarithm function is introduced in the end-member spectral difference constraint to slow down the sudden change of the trace operation of the matrix. The non-negative matrix factorization is carried out by projected gradient, and the objective function is obtained by integrating the influence of image decomposition error and endmember spectrum. The effectiveness of the algorithm is verified by simulated data experiments and real data experiments.

Description

technical field [0001] The invention relates to a hyperspectral image unmixing method based on end-member constrained non-negative matrix decomposition. Background technique [0002] Due to the limited spatial resolution of the spectral imager and the complex diversity of ground objects, some pixels of the hyperspectral image often contain multiple substances (that is, end members), and these pixels containing other end members are called mixed pixel. In order to improve the description accuracy of the real land cover, it is necessary to decompose the mixed pixel, and calculate the proportion (that is, the abundance) of a surface object type (end member) in the pixel. Unmixing of mixed pixels is an important research topic in the quantitative analysis of hyperspectral images. In 1999, Lee and Seung proposed a multiplicative iterative non-negative matrix factorization method in Nature, which attracted widespread attention. The NMF algorithm has powerful information process...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06K9/00G06T7/49
CPCG06T2207/10032G06T2207/10036G06V20/13
Inventor 赵岩张春晶曹小燕王东辉
Owner HEILONGJIANG UNIVERSITY OF SCIENCE AND TECHNOLOGY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com