Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Identification method of working modal parameters based on principal component analysis based on wavelet threshold denoising

A wavelet threshold denoising and principal component analysis technology, applied in electrical digital data processing, special data processing applications, instruments, etc., can solve problems such as unsatisfactory denoising results, distorted original input signals, etc., to achieve clear description and algorithm. The effect of clear physical meaning and improved accuracy

Active Publication Date: 2017-04-05
HUAQIAO UNIVERSITY
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

However, traditional signal denoising methods, such as Fourier transform, windowed Fourier transform, pure time domain method, pure frequency domain method, etc. have their respective application limitations, for example, Fourier transform is only suitable for stationary and linear time series analysis , when the signal contains many spikes or sudden changes, the denoising result is not ideal; the signal denoising method of the bandpass filter is effective, but this method greatly distorts the original input signal

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Identification method of working modal parameters based on principal component analysis based on wavelet threshold denoising
  • Identification method of working modal parameters based on principal component analysis based on wavelet threshold denoising
  • Identification method of working modal parameters based on principal component analysis based on wavelet threshold denoising

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

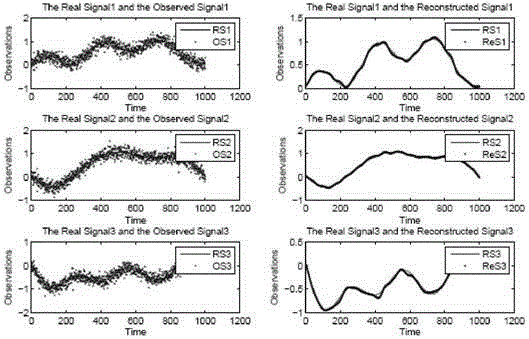
[0066] The simply supported beam with a length of 1m is divided into 1000 equal parts at equal intervals, and a total of 1001 response measuring points are generated. At the frequency points 205, 91.3, 366, 572, 824, 1121, and 22HZ, the multi-frequency sinusoidal loads with corresponding powers of 60, 30, 30, 30, 30, 30, and 30 units were respectively loaded on a 0.2m unit The response data is obtained at the point position, the sampling time is 1s, the sampling frequency interval is 4096HZ, and 1% Gaussian measurement noise is added to the response signal. Using the SymN wavelet function, the adaptive threshold is calculated by sqrt(2*log(length(X))). The experiment selects the response data of the 1st, 400th, and 500th times containing 15% Gaussian white noise as test data.

[0067] As shown in Figure 6(1), since the contribution rate of the fifth principal component is relatively small, the fifth-order mode shape is missing, which is an inherent characteristic of the princ...

Embodiment 2

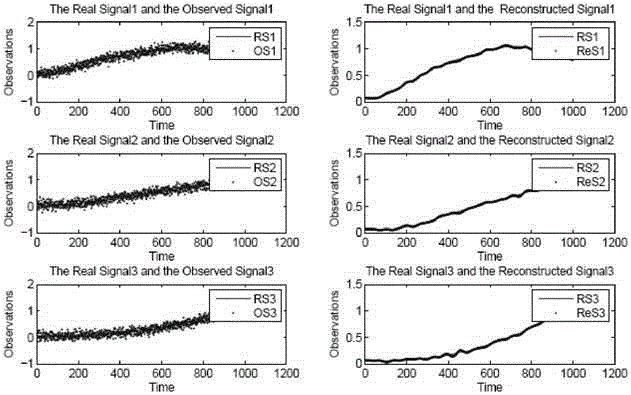
[0076] The cantilever beam with a length of 1m is divided into 1000 equal parts at equal intervals, and a total of 1001 response measurement points are generated, and a modal damping of 0.01 is added. The same white noise is applied at each node, the sampling time is 1s, the sampling frequency interval is 4096HZ, and 10% Gaussian measurement noise is added to the response signal. The SymN wavelet function is used in the experiment, and the adaptive threshold is calculated by sqrt(2*log(length(X))). The experiment selects the 20th, 1000th, 4000th response data containing 10% Gaussian white noise as test data.

[0077] As shown in Figure 6(2), comparing (a) and (c) in Figure 6(2), it is found that the PCA method is sensitive to measurement noise, which leads to mode loss in the case of noise, such as the 6th and 7th modes mode; comparing (c) and (d) in Figure 6(2), it is found that the fifth mode can be identified by PCA after wavelet denoising. As shown in Figure 7(2), compar...

Embodiment 3

[0084] A cylindrical shell with simply supported boundary conditions at both ends is excited by uniform reverberation Gaussian white noise. The parameters of the cylindrical shell are: thickness 0.005m, length 0.37m, radius 0.1825m, elastic modulus 205GPa, material Poisson's ratio 0.3, material density 7850kg / m 3 ; The modal damping ratio η is 0.03, 0.05, 0.10 respectively. The sampling frequency is set to 5120Hz, and the sampling time is set to 1s. The LMS Virtual.lab finite element method is used for calculation, and the structural displacement response data in the X, Y, and Z directions of three different damping ratios are obtained from each observation point to form a response data set in the three directions.

[0085] like Figure 8 As shown, the accuracy of the modal parameters gradually decreases with the increase of the modal damping, and the sixth mode is lost due to the small contribution rate of the principal components. Therefore, the modal parameter identifica...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to an operating modal parameter identification method for principal component analysis on basis of wavelet threshold denoising. Measurement noise in vibration response signals of a small damping mechanical structure can be effectively filtered out, the operating mode (a modal inherent frequency and modal vibration shape) of a system can be identified, operating modes (modal inherent frequency and modal vibration shapes) with small contribution amount in the response signal can be even identified, and a PCA modal parameter identification algorithm and physical significance interpretation and certification are endowed. The method is applied to three-dimensional operating modal parameter identification as well as equipment fault diagnosis and health condition monitoring. The invention further relates to an operating modal parameter analysis meter based on the method. Multiple vibrating sensors are arranged on key points of the mechanical structure, operating modal parameter identification is carried out on the vibration response signals obtained through measurement, changes of characteristics of the system structure can be understood, and the operating modal parameter analysis meter can be applied to fault diagnosis and health condition monitoring of large-scale project structures.

Description

technical field [0001] The present invention relates to a working mode parameter identification method based on principal component analysis of wavelet threshold denoising, and its application in three-dimensional working mode, and its application in equipment fault diagnosis and health status monitoring, and also relates to a method based on Modal parameter analyzer of the method. Background technique [0002] Modal analysis is a modern method to study the dynamic characteristics of structures, and it is the application of system identification method in the field of engineering vibration. Accurate identification of modal parameters is of great significance for structural damage diagnosis, health monitoring, optimal design of mechanical equipment, and structural dynamic characteristics. The traditional experimental modal analysis method is to apply artificial excitation to the structure under laboratory conditions, and obtain the frequency characteristics between any two p...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F19/00
Inventor 缑锦王成赖雄鸣崔长彩杜吉祥王靖官威候峰
Owner HUAQIAO UNIVERSITY
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com