Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

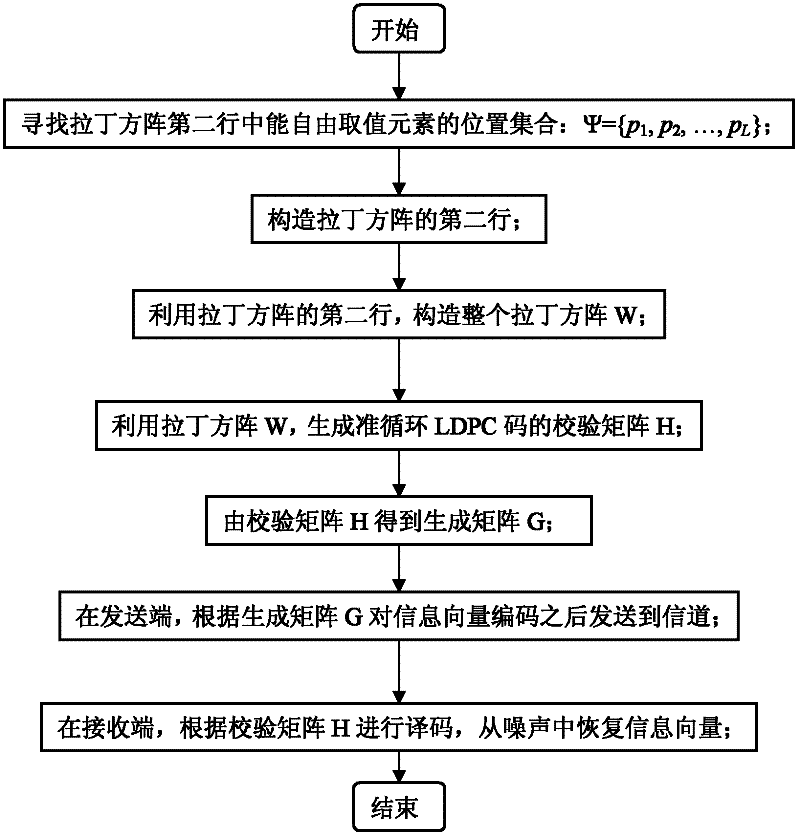
Error correction method by using quasi-cyclic LDPC code based on Latin square

A technology of LDPC code and error correction method, which is applied in the field of quasi-cyclic LDPC code and channel quasi-cyclic LDPC code error correction, can solve the problems of not the best performance, performance difference, and high complexity, and achieve low error floor performance and complex The effect of low degree and less redundancy

Inactive Publication Date: 2012-04-18
XIDIAN UNIV
View PDF1 Cites 8 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0005] However, there are multiple Latin square matrices of the same order that satisfy the row-column constraint relationship, and the quasi-cyclic LDPC codes constructed based on them have different performances in the high SNR area, and Lin Shu only gave one of them in the construction special case, the performance of this special case is not the best, and this special case cannot provide a wider space for further searching for codewords with low error floors
On the other hand, to find all Latin square matrices of the same order that satisfy the row-column constraints, if full search is used, the high complexity cannot be realized

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Error correction method by using quasi-cyclic LDPC code based on Latin square
  • Error correction method by using quasi-cyclic LDPC code based on Latin square
  • Error correction method by using quasi-cyclic LDPC code based on Latin square

Examples

Experimental program
Comparison scheme
Effect test

example 1

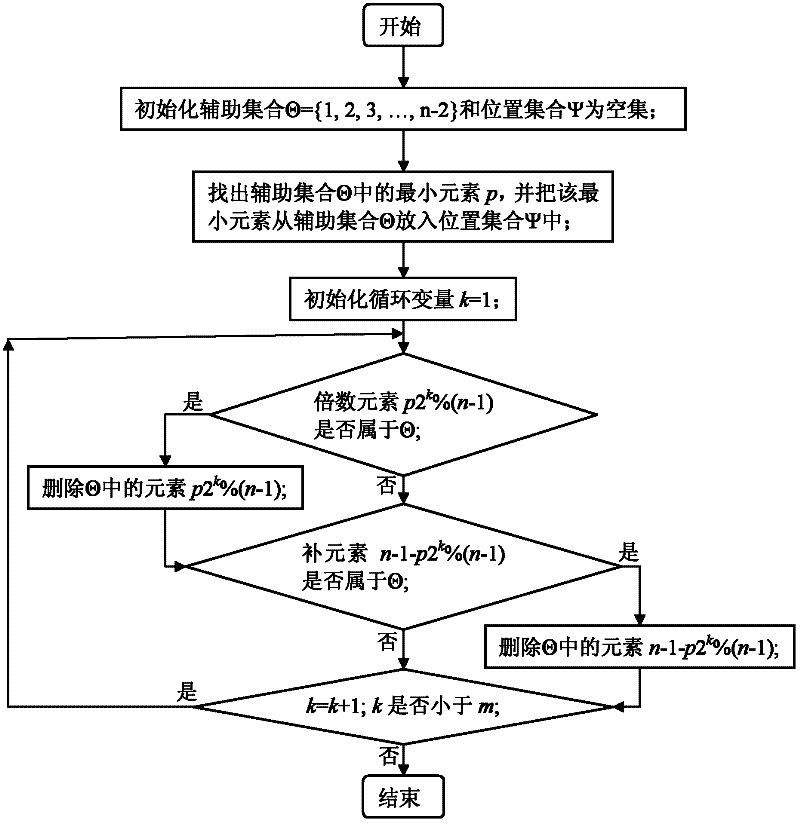
[0043] Example 1: For 2 that satisfy the row and column constraints 3 Order Latin square matrix, m=3, n=8, the elements in the fourth column of the second row are twice the elements in the third column; the elements in the sixth column are four times the elements in the third column; the elements in the eighth column It is the complement element of the element in the third column, that is, n-1 minus the element in the third column; the element in the seventh column is the complement element of the element in the fourth column, that is, n-1 minus the element in the fourth column; the above relationships are all in the modulo n- 1 under. Due to the existence of the above relationship, it is only necessary to determine the values ​​of the elements in the third column and the fifth column to obtain the values ​​of all other positions, that is, the position set Ψ={1, 3}, L=2.

[0044] Step 2, construct the second row of the Latin square matrix:

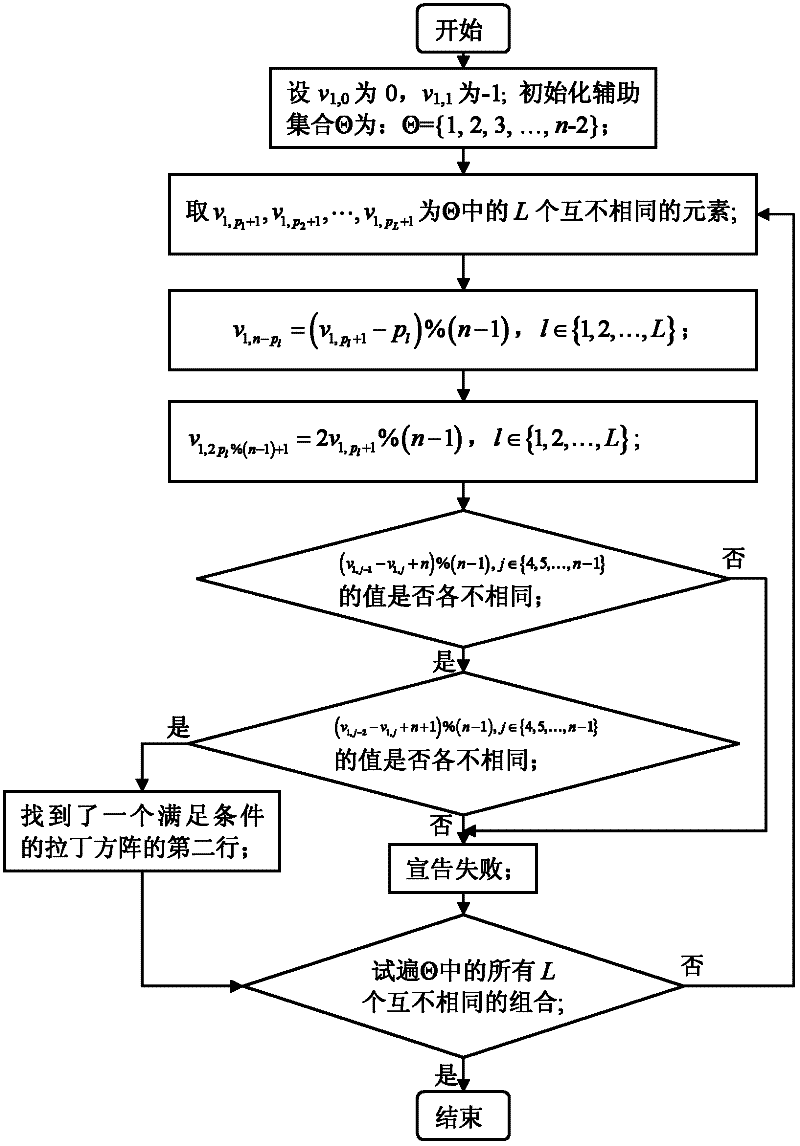
[0045] see image 3 As shown, th...

example 2

[0053] Example 2: For the 2 that satisfies the row and column constraints 3 Order Latin square matrix, m=3, n=8, according to the constraint relationship between the elements of each position described in Example 1, if the value of the third column element is 3, then the second behavior of the entire Latin square matrix can be obtained [0 -1 3 6 1 5 4 2].

[0054] Step 3, use the second row of the Latin square matrix to construct the entire Latin square matrix W:

[0055] (3a) The exchange of rows and columns of the Latin square matrix will not affect the performance of the quasi-cyclic LDPC code generated by it, so firstly, after the exchange of rows and columns, the elements on the diagonal are set to v i，i = -1, i ∈ {1, 2, ..., n-1};

[0056] (3b) Starting from the third row of the W matrix, it is generated row by row, and the element in row i+1 and column j+1 is generated from the element in row i and column j according to the following relationship:

[0057] v i，j =(v...

example 3

[0063] Example 3: For 2 that satisfy the row and column constraints 3 Order Latin square matrix, m=3, n=8, according to the second line of the given Latin square matrix of example 2, obtain whole Latin square matrix as follows:

[0064] - 1 0 1 2 3 4 5 6 0 - 1 3 6 1 5 4 2 1 ...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses an error correction method by using a quasi-cyclic LDPC code based on a Latin square, mainly solving a problem that in the prior art a simple method of finding a Latin square totally satisfying a row column constraint relation is lacked. The method comprises the following steps: (1) searching a position set Psi of elements which are free in value selection in a second row of the Latin square; (2) constructing the second row of the Latin square; (3) constructing a whole Latin square W; (4) generating a verification matrix H of a quasi-cyclic LDPC code; (5) obtaining a generation matrix G according to the verification matrix H; (6) at a sending terminal, coding information with the generation matrix G and sending the information to a channel; (7) at a receiving terminal, carrying out decoding according to the verification matrix H, and recovering information from noise. Simulation shows that, error correction performance of constructed quasi-cyclic LDPC code based on the Latin square is excellent, and the method can be used for carrying out error correction in a communication or digital storage system needing high reliability.

Description

technical field [0001] The invention belongs to the communication field, and relates to a channel quasi-cyclic LDPC code error correction method, in particular to constructing a class of quasi-cyclic LDPC codes with Latin square matrices satisfying row-column constraints, which are used in communication or digital storage systems requiring high reliability Make corrections. Background technique [0002] The modern information society is changing with each passing day, and communication technology is developing rapidly. The most basic purpose of communication is to realize the effectiveness and reliability of information transmission. The way to improve the effectiveness of information transmission is to increase spectral efficiency, and the way to improve reliability is to use error-correcting code technology. The error correction codes used in various modern communication systems are mainly iterative decodable codes represented by Turbo codes and LDPC codes. [0003] LDP...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H03M13/11
Inventor 车书玲王新梅
Owner XIDIAN UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com