Supercharge Your Innovation With Domain-Expert AI Agents!

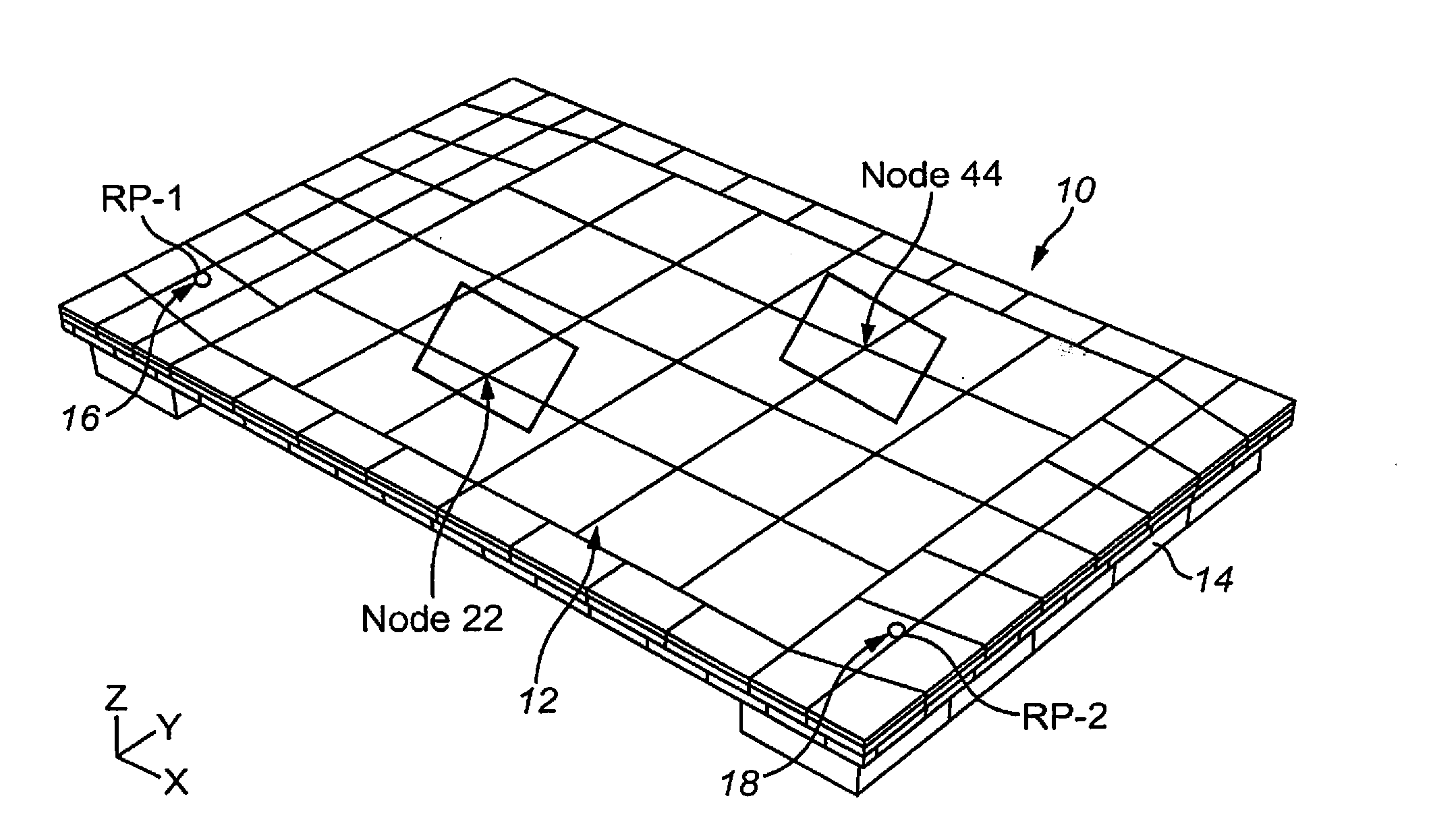
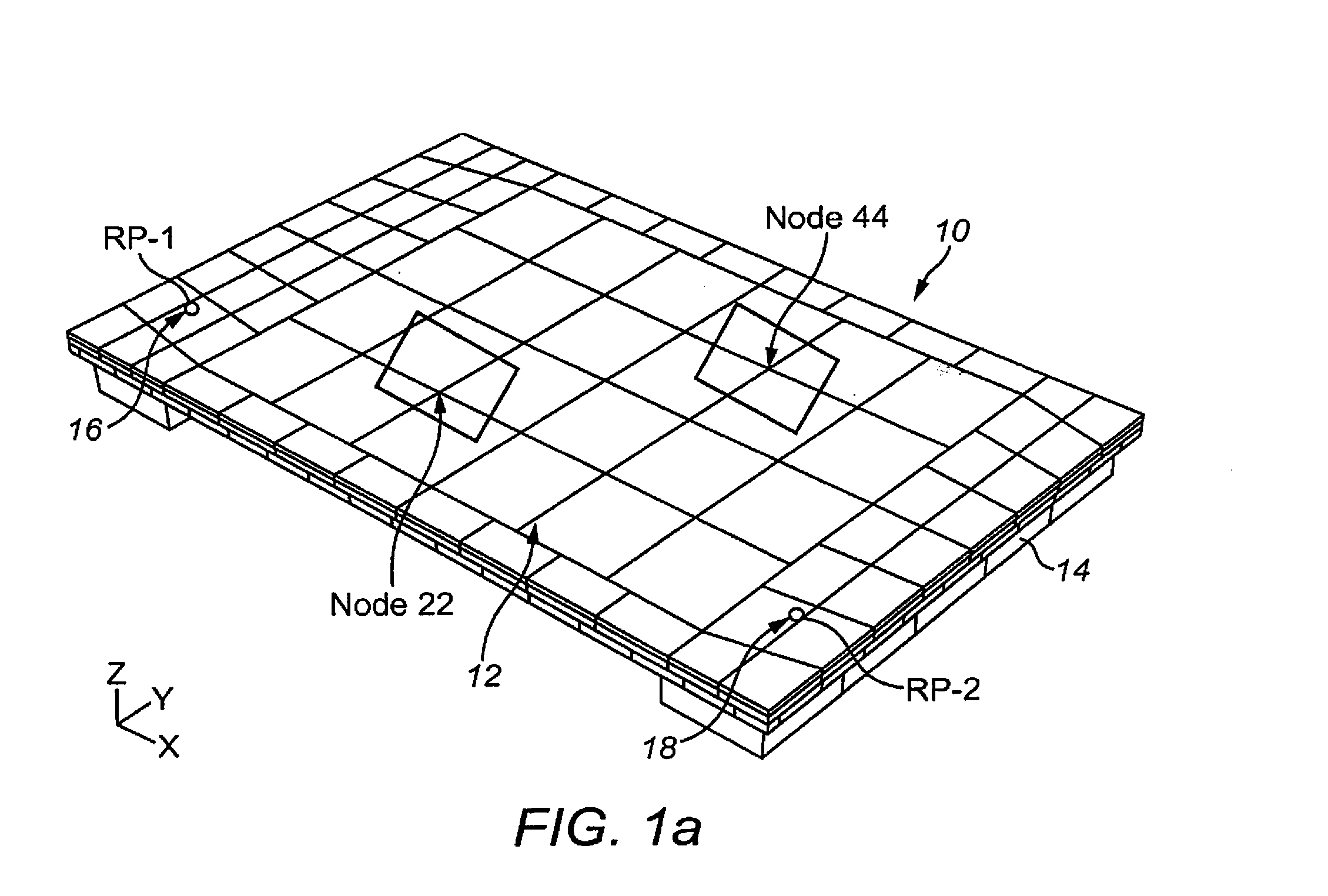
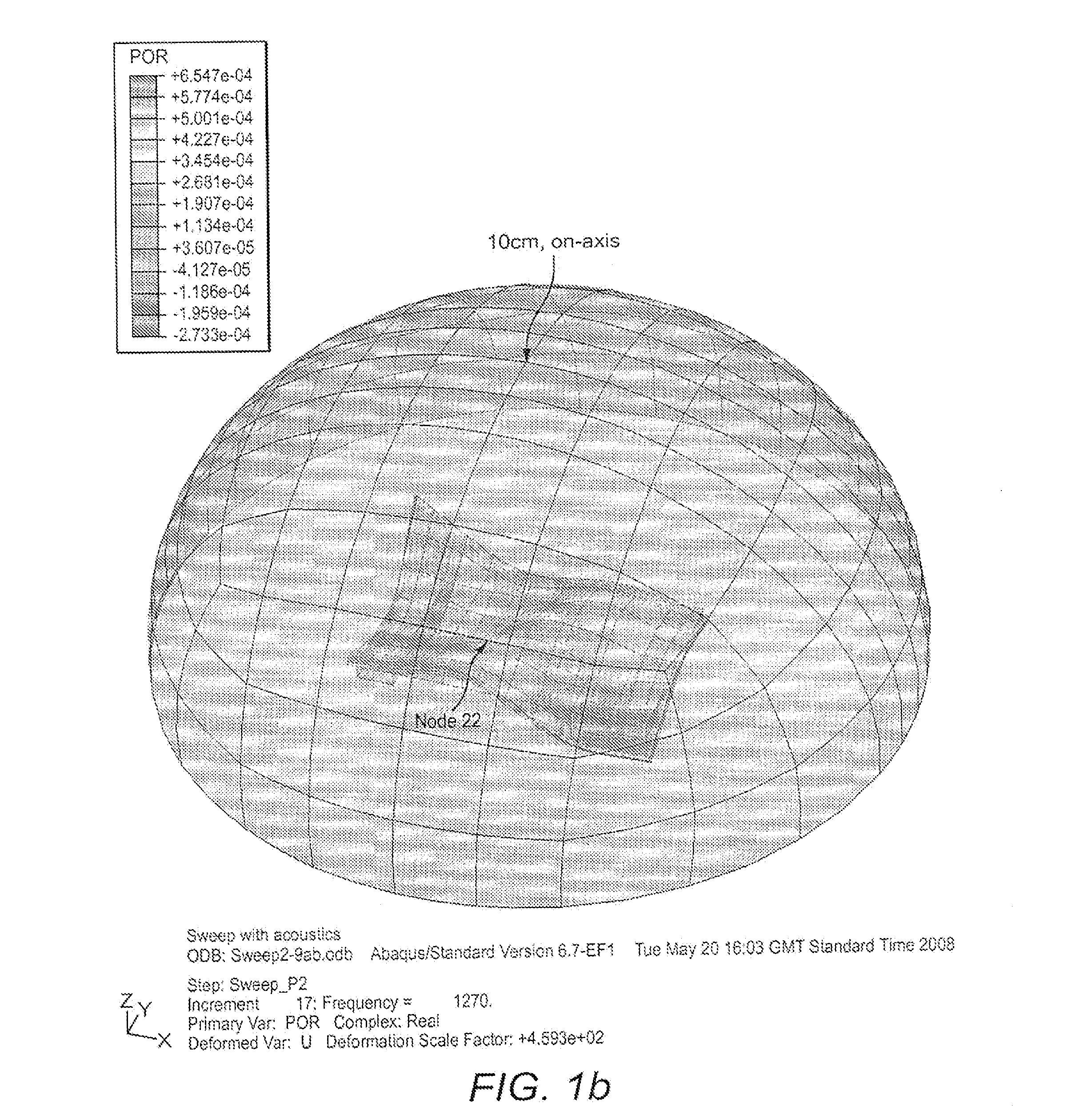
Touch Sensitive Device

Inactive Publication Date: 2015-10-01
GOOGLE LLC
View PDF3 Cites 18 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Benefits of technology

The solution achieves simultaneous multi-region haptics with improved signal-to-noise ratio and reduced residual vibrations, providing clear and distinct tactile feedback at each sensing area even when multiple locations are touched simultaneously.

Problems solved by technology

Anywhere else on the panel will experience a combination of the signals, but this is unimportant.

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Touch Sensitive Device
  • Touch Sensitive Device
  • Touch Sensitive Device

Examples

Experimental program
Comparison scheme
Effect test

example 1

m=3, n=2

[0195]Output 1 transfer admittances: P1—1=0.472+0.00344j

[0196]Output 2 transfer admittances: P1—2=−0.206−0.195j

[0197]Output 1 transfer admittances: P2—1=0.479−0.129j

[0198]Output 2 transfer admittances: P2—2=0.262+0.000274j

[0199]Output 1 transfer admittance: P3—1=−0.067−0.180j

[0200]Output 2 transfer admittance: P3—2=0.264+0.0014j

[0201]All at Once

M1+M2=(0.3030.171-0.012j-0.087-0.034j0.171+0.012j0.3150.061-0.095j-0.087+0.034j0.061+0.095j0.107);

|M1+M2|=0

[0202]M1+M2: eigenvalues are 0, 0.218 and 0.506:

[0203]Eigenvector after scaling: (0.434−0.011j, −0.418+0.199j, 0.764+0.115j)

[0204]One at a Time

[0205]Solve output 1, and then output 2. As 3>2 we should get the same answer.

M1=(0.2230.226-0.063j-0.032-0.085j0.226+0.063j0.246-0.009-0.095j-0.032+0.085j-0.009+0.095j0.037);

|M1|=0

[0206]M1: eigenvalues are 0, 0 and 0.506:

[0207]Eigenvector V1: (0.748, −0.596−0.165j, 0.085−0.224j)

[0208]Eigenvector V2: (−0.062+0.026j, 0.096+0.350j, 0.929)

[0209]New problem; select a and b such that a·V1+b·V2...

example 2

m=3, n>=3

[0221]Here we have 1 acoustic pressure output and a number of velocity outputs.

[0222]Acoustic scaled error matrix is M1, summed velocity scaled error matrix is M2.

M1=(3.928-2.667+2.473j-2.674+2.506j-2.667-2.473j3.3673.393-0.018j-2.674-2.506j3.393+0.018j3.418);

|M1|=0

[0223]M2=(1.0230.602+0.112j-0.528+0.409j0.602+0.112j0.977-1.144+0.205j-0.528-0.409j-1.144-0.205j5.473);

|M2|=2.510

[0224]All at Once

[0225]All n output error matrices are summed and the eigenvector corresponding to the lowest eigenvalue is found.

[0226]Eigenvalues (M1+M2)=1.146, 3.869, 13.173

[0227]Solution=(0.739−0.235j, 0.483+0.306j, 0.246+0.104j)

[0228]One at a Time

[0229]Actually, we solve just the acoustics problem, then do the rest all at once. That way, the acoustics problem is solved exactly.

[0230]Eigenvalues (M1)=0, 0, 10.714

[0231]V1=(0.770−0.199j, 0.376+0.202j, 0.377+0.206j)

[0232]V2=(0.097−0.071j, 0.765+0.010j, −0.632+0.0016j)

[0233]As V1 and V2 both correspond to a zero eigenvalue, a·V1+b·V2 is also an eigenve...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A touch sensitive device comprising a panel capable of supporting bending waves, a user-accessible touch sensitive screen on or forming part of a face of the panel, the touch sensitive screen having a plurality of different sensing areas, a plurality of vibration exciters coupled to the panel to apply bending waves to the panel to provide tactile feedback at the plurality of sensing areas in response to the user touching a sensing area, and signal processing means arranged to apply signals to the vibration exciters so as to steer bending waves applied to the panel by the plurality of vibration exciters whereby the amplitude of the applied bending waves is maximised at the sensing area touched by the user and reduced or minimised at each other sensing area.

Description

CROSS-REFERENCE TO RELATED APPLICATIONS[0001]This is a continuation application of U.S. patent application Ser. No. 12 / 921,935 filed Dec. 13, 2010 which is the U.S. National Phase of PCT Application No. JP2009 / 064365 filed 7 Aug. 2009 which claims priority to British Patent Application No. 0818117.4 filed 3 Oct. 2008, each of which are incorporated herein by reference.TECHNICAL FIELD[0002]The invention relates to touch sensitive devices including touch sensitive screens or panels.BACKGROUND ART[0003]U.S. Pat. No. 4,885,565, U.S. Pat. No. 5,638,060, U.S. Pat. No. 5,977,867, US2002 / 0075135 describe touch-operated apparatus having tactile feedback for a user when touched. In U.S. Pat. No. 4,885,565 an actuator is provided for imparting motion to the CRT when the actuator is energized to provide tactile feedback. In U.S. Pat. No. 5,638,060, a voltage is applied to a piezo-electric element which form a switch to vibrate the element to apply a reaction force to a user's finger. In U.S. Pa...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(United States)
IPC IPC(8): G06F3/01G06F3/041
CPCG06F3/0416G06F3/016G06F3/043G06F3/04166G06F3/0418H01H13/14H01H13/70
Inventor HARRIS, NEIL JOHN
Owner GOOGLE LLC
Features
  • R&D
  • Intellectual Property
  • Life Sciences
  • Materials
  • Tech Scout
Why Patsnap Eureka
  • Unparalleled Data Quality
  • Higher Quality Content
  • 60% Fewer Hallucinations
Social media
Patsnap Eureka Blog
Learn More

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com