Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

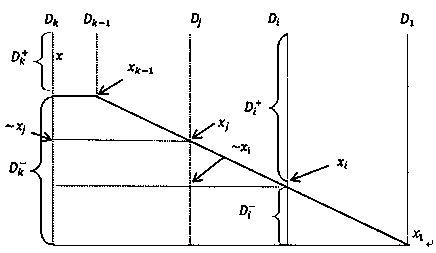
Paradox separation deductive reasoning method based on extended triangle in propositional logic

A technology of propositional logic and reasoning method, applied in the direction of reasoning method, etc., can solve the problems that the ability and efficiency cannot meet the objective needs, cannot reflect the cooperative logical relationship of multiple clauses, and the clause set S cannot be satisfied, etc.

Pending Publication Date: 2018-11-23
SOUTHWEST JIAOTONG UNIV
View PDF0 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Binary resolution selects two clauses with complementary pairs from the clause set S to be determined each time, deletes the complementary pair from the two clauses, and adds the new clauses formed by the disjunction of the remaining words into the clause set S, and repeats As above process, until an empty clause is obtained, it can be determined that the clause set S is unsatisfiable
[0005] Although the automatic reasoning system based on the resolution principle has made many achievements, it is still far from meeting the objective needs in terms of ability and efficiency. Only in the internationally renowned problem bank TPTP in the field of automatic reasoning, there are a large number of the most difficult (Rating1) problems that have not been solved so far.
In the resolution method, because each deduction has and can only have two clauses involved, it cannot reflect the cooperative logical relationship between multiple clauses
The reasoning mechanism of binary resolution seriously restricts the further improvement of the ability and efficiency of automatic reasoning

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Paradox separation deductive reasoning method based on extended triangle in propositional logic
  • Paradox separation deductive reasoning method based on extended triangle in propositional logic
  • Paradox separation deductive reasoning method based on extended triangle in propositional logic

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

[0063] Let clause set S={C in propositional logic 1 ,C 2 ,C 3 ,C 4 ,C 5 ,C 6 ,C 7 ,C 8 ,C 9 ,C 10}, C 1 = 1, C 2 = 2, C 3 =~1∨~2∨3, C 4 =~1∨4, C 5 =~4∨5,C 6 =~3∨~5,C 7 =~3∨7, C 8 =~5∨~7,C 9 =~3∨~4, C 10 =~2∨~7; wherein 1, 2, 3, 4, 5, 6, 7 are proposition variables. For the clause set S, there are two deduction based on the extended triangle method as follows.

[0064] Approach 1: Select clause C 1 ,C 2 ,C 3 ,C 7 ,C 10 , from these clauses construct the extended triangular contradiction in,

[0065]

[0066] The corresponding contradictory separation formula is an empty clause.

[0067] Approach 2: Select clause C 1 ,C 2 ,C 3 ,C 4 ,C 5 ,C 6 , from these clauses construct the extended triangular contradiction in,

[0068]

[0069] The corresponding contradictory separation formula is an empty clause.

[0070] The above two methods can obtain an extended triangle with no words above the main boundary line, that is, the separation of cont...

Embodiment 2

[0072] Let clause set S={C in propositional logic 1 ,C 2 ,C 3 ,C 4 ,C 5 ,C 6 ,C 7}, C1 =~3∨~7,C 2 =2∨3∨5∨~6,C 3 =1∨~2∨5∨~7,C 4 =1∨3∨~5,C 5 =3∨4∨6,C 6 =~1∨3,C 7 =7; 1, 2, 3, 4, 5, 6, 7 are propositional variables. For the clause set S, the following extended triangle can be constructed.

[0073] Practice: select clause C 1 ,C 2 ,C 3 ,C 4 ,C 5 ,C 6 ,C 7 , from these clauses construct the extended triangular contradiction in,

[0074]

[0075] The corresponding contradictory separation formula is

[0076] because And all the clauses in S are used in the construction of the extended triangular contradiction, so it can be concluded that the clause set S is satisfiable, and a satisfiable example of S is obtained: ~3, ~6, ~2, ~5,4, ~1,7.

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a paradox separation deductive reasoning method based on an extended triangle in propositional logic. The method comprises the following steps that: for a clause set S in the propositional logic, constructing an extended triangle paradox, forming a paradox separation formula, and judging clause set attributes according to the paradox separation formula; if a judgment resultshows that the clause set can not be satisfied, stopping; otherwise, adding the obtained paradox separation formula into an original clause set to form a new clause set; and then, constructing and separating the extended triangle paradox, and stopping until the judgment conclusion of clause set attributes is obtained or a set condition is met. The invention provides an effective dynamic automaticdeductive reasoning method based on paradox separation, a collaborative logic relationship among a plurality of clauses can be effectively described, and the method can be applied to fields includingprogram verification, automated theorem proving and the like.

Description

technical field [0001] The invention belongs to the technical field of automatic deductive reasoning based on logic, and relates to a multivariate dynamic automatic deductive reasoning method based on extended triangle-based contradiction separation in propositional logic. Background technique [0002] A large number of scientific problems in the fields of logic, mathematics, system optimization, artificial intelligence, computer science, etc. can be formalized into logical representations. One of the essences of solving these problems is to analyze the attributes of the corresponding logical formulas (satisfiability or unsatisfiability (constant False)), but because of its abstraction, complexity, and scale, it is impossible to effectively implement logical reasoning and solution artificially, so it needs to be automatically judged by a computer. Automatic reasoning is the process of formalizing the reasoning process through a series of symbols, and making the computer auto...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): G06N5/04
CPCG06N5/042G06N5/045
Inventor 徐扬陈树伟刘军何星星钟小梅
Owner SOUTHWEST JIAOTONG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com