Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Robust estimation method for estimating equation containing non-ignorable missing data

A technique for missing data and estimating equations, used in complex mathematical operations, etc.

Inactive Publication Date: 2016-09-07
CHINA UNIV OF PETROLEUM (EAST CHINA)
View PDF5 Cites 1 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0007] The purpose of the present invention is to provide a robust estimation method for estimation equations containing non-negligible missing data, which avoids Using non-parametric kernel estimation to calculate conditional expectations, there will be no "dimensional curse" phenomenon, and it can be applied to the estimation problem of estimation equations with non-negligible missing data in the presence of high-dimensional covariates

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Robust estimation method for estimating equation containing non-ignorable missing data
  • Robust estimation method for estimating equation containing non-ignorable missing data
  • Robust estimation method for estimating equation containing non-ignorable missing data

Examples

Experimental program
Comparison scheme
Effect test

Embodiment 1

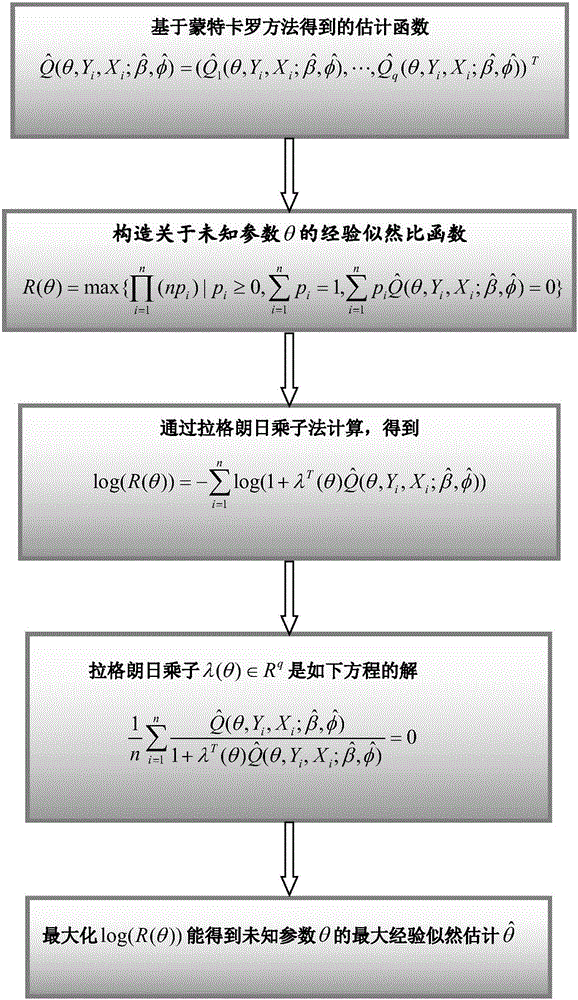
[0084] Embodiment 1: Taking the estimation of the mean value of the response variable θ=E(Y) in the linear regression model Y=1.2+X+ε under the condition that the response variable has non-negligible missing data as an example, the estimation method of the present invention is described in detail.

[0085] The estimation equation Q(θ,Y,X)=Y-θ is selected, and 5000 random samples of capacity 200 are randomly and independently drawn from the linear model. The missing data of the response variable satisfies: the indicative variable δ of the response variable i Respectively from the following according to the probability of π 1 and π 2 The Bernoulli distribution yields:

[0086] π 1 ( X i , Y i ...

Embodiment 2

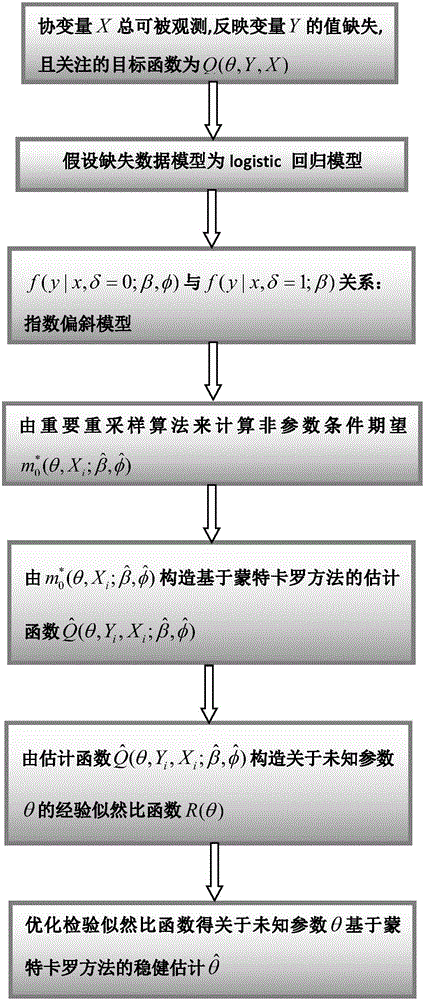
[0099] Example 2: Non-linear regression model with non-negligible missing data in the response variable As an example, the estimation method of the present invention will be described in detail.

[0100] random sample {(X i ,Y i ):i=1,...,n} to the above-mentioned nonlinear model. For each i, X i is a sample from a uniform distribution U(0,1), given X i , Y i is from a normal distribution N(θX i +exp(θX i ),1) and θ=1 samples. CovariateX i is always observable, but Y i There is something missing. According to probability π(X i ,Y i )=P(δ i =1|X i ,Y i ) yields the reflection variable Y from a Bernoulli distribution i missing indicative variable. Examine four missing data mechanisms:

[0101]

[0102]

[0103]

[0104]

[0105] Among them, (φ 0 ,φ 1 ,φ 2 ,φ 3 ) = (1.5, 0.15, 0.5, 0.25).

[0106] They are all non-negligible missing data. The first two satisfy the hypothetical missing data model; the latter two do not satisfy the missing data m...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention relates to a robust estimation method for an estimating equation containing non-ignorable missing data. The method includes the steps: calculating a conditional expectation m (Theta, x) contained in an interpolation estimating equation Q<Tilde> (Theta, Y, X) through an important resample algorithm based on a given estimating equation Q (Theta, Y, X) when a non-ignorable missing data model is a logistic regression model, and then obtaining a modified estimating equation Q<hat> (Theta, Y, X); and acquiring robust experience likelihood estimation of an unknown parameter Theta of the estimating equation through an experience likelihood method based on the modified estimating equation Q<hat> (Theta, Y, X). The method interpolates the estimating equation containing the missing data through the estimating equation rather than the missing value interpolation method, performs robust estimation through the experience likelihood method, can successfully avoid the problem that the non-parametric kernel estimation method causes dimension curse when the dimensionality of a concomitant variable is high, and greatly improve the accuracy of data treatment when the non-ignorable missing data exists, and improve the accuracy of prediction.

Description

technical field [0001] The invention belongs to the field of data mining and machine learning, and relates to data mining and data processing methods, in particular to a robust estimation method for estimation equations containing non-negligible missing data. Background technique [0002] Most of the classic statistical methods and theories are based on complete data analysis. However, in practice, missing data generally occurs in many practical problems, such as public opinion surveys, market research, mailed questionnaires, social economic research, medical research, The problem of missing data often occurs in observational studies and other scientific experiments. In this case, standard statistical methods cannot be directly applied to the statistical analysis of these incomplete data. At present, most of the processing of incomplete data assumes that the missing data mechanism is negligible, and individuals with missing data are often deleted, and only the data group co...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Applications(China)
IPC IPC(8): G06F17/11
CPCG06F17/11
Inventor 宋允全
Owner CHINA UNIV OF PETROLEUM (EAST CHINA)
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com