Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Elliptic curve encryption method comprising error detection

An elliptic curve encryption, elliptic curve technology, used in the countermeasures of attacking encryption mechanisms, public keys for secure communication, instruments, etc.

Active Publication Date: 2016-02-17
RAMBUS INC
View PDF9 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Therefore, it may not be effective to detect error injection only at the end of computation

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Elliptic curve encryption method comprising error detection
  • Elliptic curve encryption method comprising error detection
  • Elliptic curve encryption method comprising error detection

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

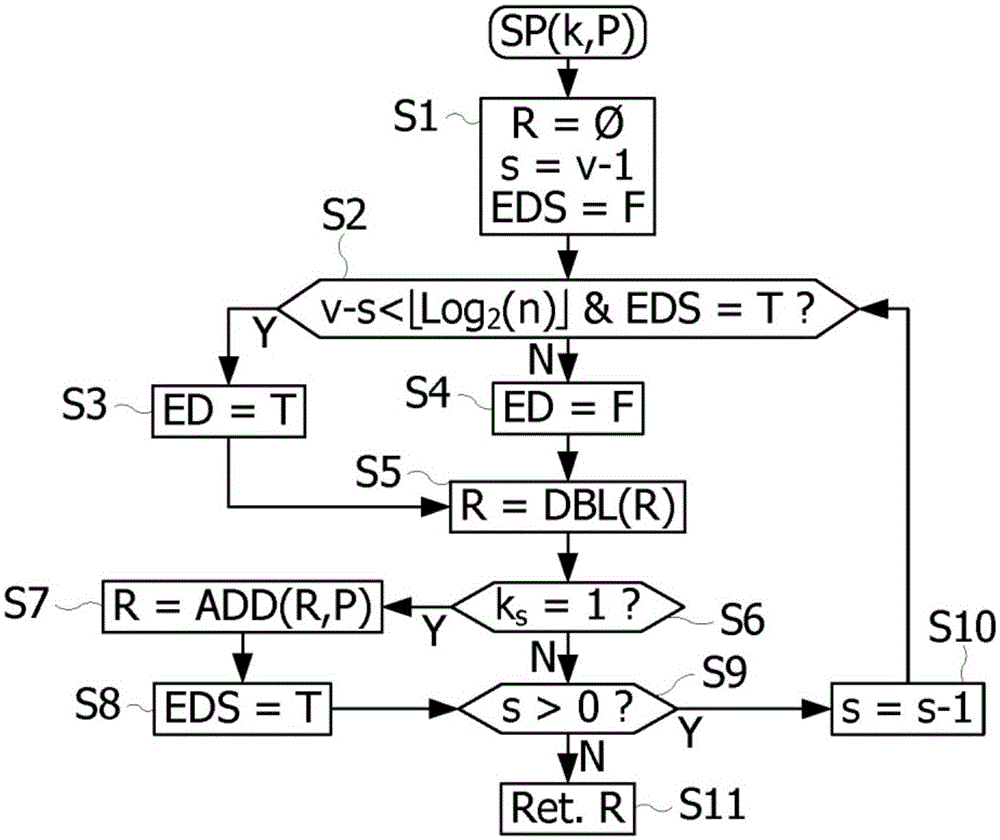
[0025] Elliptic curve cryptosystems generally require the definition of so-called "domain" parameters. In GF(p) or GF(2 m ) type Galois field, these parameters include: a large prime number p or a large integer m; the generation point or base point G of coordinates Gx and Gy in the Galois field; the prime number n called "order" of point G, such that is the point at infinity or the neutral element in the Galois field; the parameters defining the elliptic curve; the number f called the "cofactor", generally equal to 1, 2, or 4, so that f·n represents the number of points of the elliptic curve. In a Galois field of type GF(p), an elliptic curve may for example have a shape such as E(a,b):y 2 =x 3 The equation of +ax+b. In this elliptic curve, the opposite point of a point P with affine coordinates (x, y) is a point -P with coordinates (x, -y).

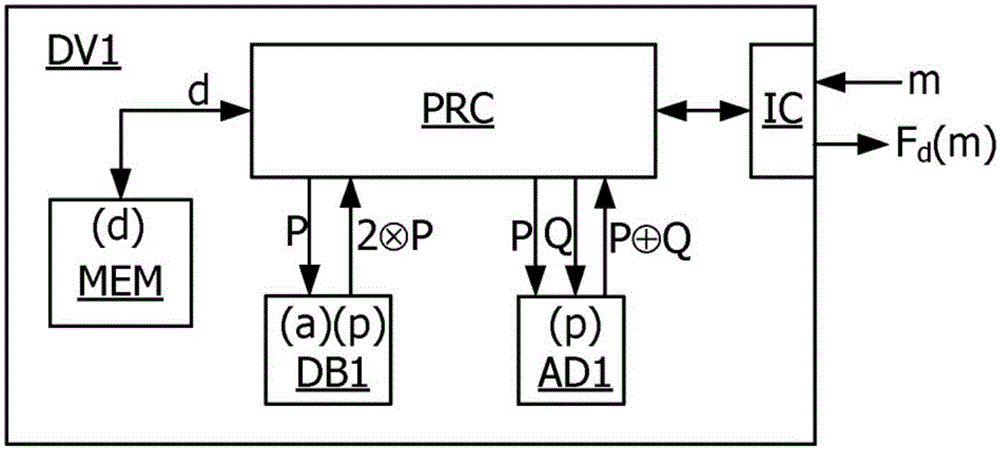
[0026] figure 1 An electronic device DV1 is represented in the form of a block diagram, configured to perform cryptographic cal...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

A method in an elliptic curve cryptographic system, the method being executed by an electronic device and including a multiplication operation of multiplying a point of an elliptic curve by a scalar number, the point having affine coordinates belonging to a Galois field, the multiplication operation including steps of detecting the appearance of a point at infinity during intermediate calculations of the multiplication operation, and of activating an error signal if the point at infinity is detected and if the number of bits of the scalar number processed by the multiplication operation is lower than the rank of the most significant bit of an order of a base point of the cryptographic system.

Description

technical field [0001] The present invention relates to the implementation of elliptic curve encryption methods in electronic devices, and in particular to the detection of attacks by such devices during the execution of cryptographic calculations. Background technique [0002] Various known elliptic curve encryption methods are based on scalar multiplication whose mathematical expression is: (k times), P is the point selected on the elliptic curve, k is an integer, is an addition operator applied to points of an elliptic curve. The number k can be used, for example, as a private key, the point obtained from this operation Or one of the affine coordinates of the point can be used as the public key corresponding to the private key k. In fact, from the result Finding the value of the number k in the coordinates of and point P is very difficult, especially when the number k and the coordinates of point P are chosen high enough. This operation is used, for example, duri...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
IPC IPC(8): H04L9/30
CPCG06F7/725G06F2207/7271H04L9/004H04L9/3066
Inventor V·杜帕奎斯
Owner RAMBUS INC
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com