Method of building coefficient transfer matrix between Zernike polynomial aberration model and Walsh function aberration model
A technology of conversion matrix and coefficient matrix, which is applied in the direction of measuring devices, instruments, scientific instruments, etc., can solve the problems of weakening the speed advantage of the method, the disadvantage of wavefront phase restoration effect, and large residual error, so as to improve the wavefront restoration effect and improve The effect of the conflict between wavefront restoration accuracy, avoidance accuracy, and speed
- Summary
- Abstract
- Description
- Claims
- Application Information
AI Technical Summary
Problems solved by technology
Method used
Image
Examples
Embodiment Construction
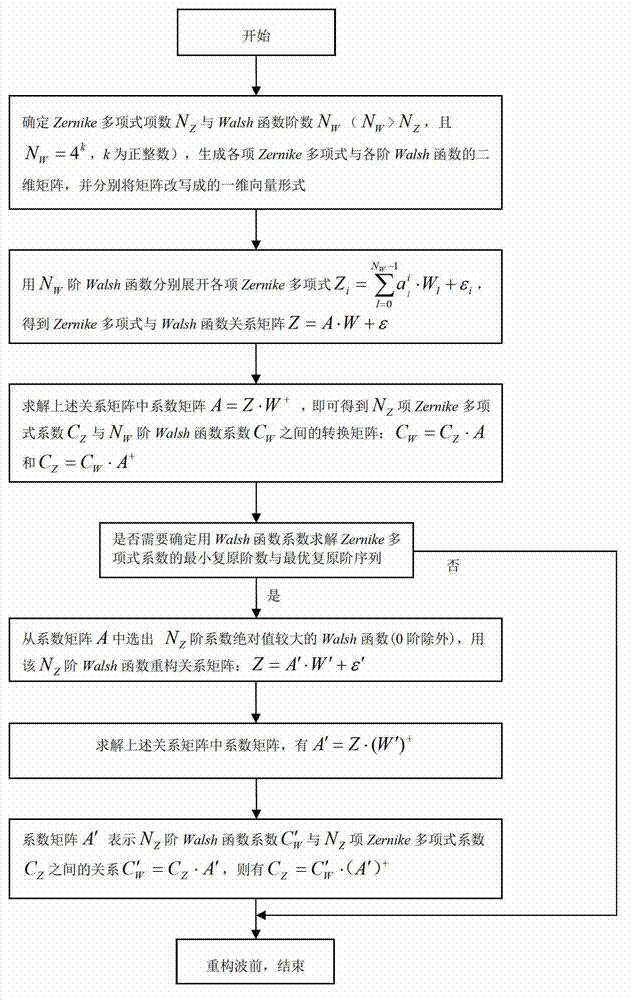
[0037] In order to make the object, technical solution and advantages of the present invention clearer, the present invention will be described in further detail below in conjunction with specific embodiments and with reference to the accompanying drawings.
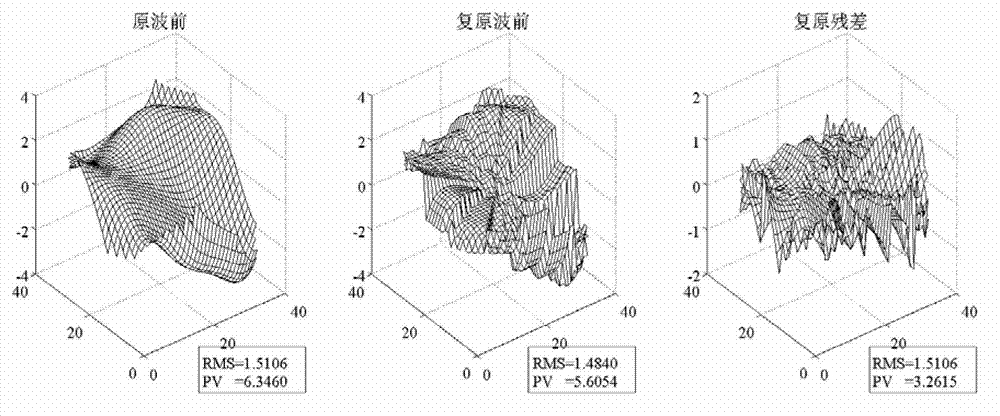
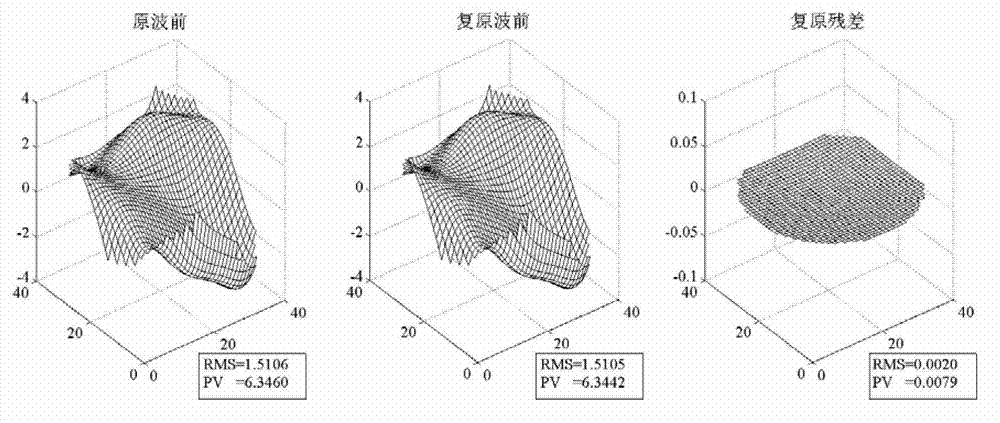
[0038] Generally, the wavefront phase distribution is considered to be continuous, and the Zernike polynomial distribution of the low-order term is consistent with the common aberration distribution of the actual optical system. Therefore, the Zernike polynomial, as an aberration mode, has been used to describe the wavefront phase and image. The most classic way to differentiate type information. Common wavefront sensors (such as the Hartmann-Shack wavefront sensor) not only give the wavefront phase distribution form, but also provide the information of various Zernike polynomial coefficients contained in the wavefront phase, allowing users to clarify the image in the wavefront phase Different types and ingredients. Howe...
PUM
 Login to View More
Login to View More Abstract
Description
Claims
Application Information
 Login to View More
Login to View More - R&D
- Intellectual Property
- Life Sciences
- Materials
- Tech Scout
- Unparalleled Data Quality
- Higher Quality Content
- 60% Fewer Hallucinations
Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.
© 2025 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com