Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

Compressed Sensing Noisy Signal Restoration Method Based on Threshold Shrinkage Iteration

A threshold shrinkage iteration and compressed sensing technology, applied in the field of signal processing, can solve problems such as complex algorithms and inability to guarantee accuracy, and achieve the effects of strong robustness, fast calculation speed, and good recovery ability.

Inactive Publication Date: 2017-03-29
XIAN UNIV OF TECH
View PDF1 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

Commonly used convex optimization methods include gradient descent method, homotopy method, LASSO (LeastAbsolute Shrinkage and Selection Operator) operator method, weighted least square method, minimum angle regression method, etc. Accuracy cannot be guaranteed for larger

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • Compressed Sensing Noisy Signal Restoration Method Based on Threshold Shrinkage Iteration
  • Compressed Sensing Noisy Signal Restoration Method Based on Threshold Shrinkage Iteration
  • Compressed Sensing Noisy Signal Restoration Method Based on Threshold Shrinkage Iteration

Examples

Experimental program
Comparison scheme
Effect test

Embodiment Construction

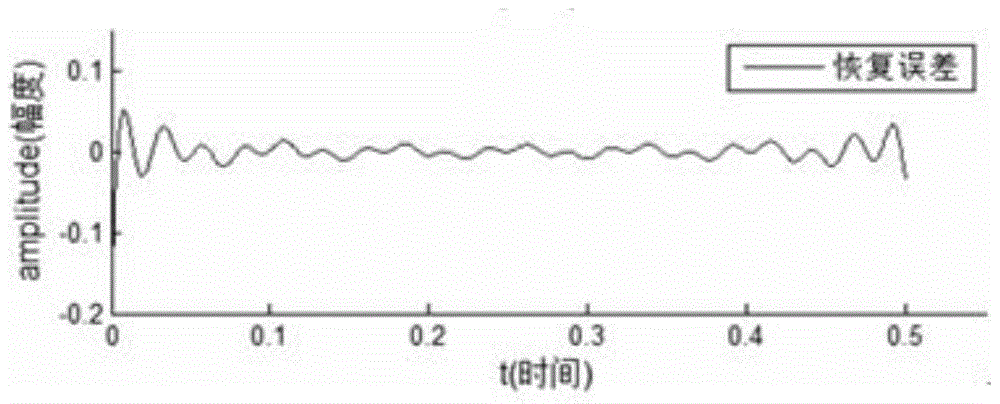
[0050] The present invention will be described in detail below in conjunction with the accompanying drawings and specific embodiments.

[0051] First, a restoration model of the noise introduced after compression is established.

[0052] The mathematical model of compressed sensing without noise is

[0053] y=θΦx (1)

[0054] In the formula, x is the original signal of n×1, y is the compressed signal of m×1, Φ is a sparse basis, which is an n×n orthogonal transformation matrix, and the function is to sparse x to make x become non-zero A signal whose number of elements r is much smaller than the number of zero elements; θ is an m×n measurement matrix, also known as a reconstruction operator, whose function is to compress the sparse signal data volume from n to m, m<

[0055] If the measured signal x of length n is r-sparse under the sparse base Φ uncorrelated with θ, the measured value y is known and satisfies

[0056] m≥C·μ 2 (θ,Φ)·r·l...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

Disclosed is a restoration method for a compressed sensing signal with noise based on threshold value shrinkage iteration. The method comprises the steps of restoring the signal, obtained after compressed sensing, with the introduced noise as a research object, building a restoring model for the compressed signal with the noise, and using the threshold value shrinkage iteration algorithm for restoring the signal with the noise. According to the problem that noise widely exists in a project, the signal, obtained after compressed sensing, with the introduced noise is used as the research object, the restoration model for the signal is built, the quite good restoration capacity for ideal sparse signals is achieved, and the computation speed is high. By the adoption of the restoration method for the compressed sensing signal with the noise based on threshold value shrinkage iteration, robustness is improved by increasing the number of iterations and the number of rows of measurement matrixes, and the restoration error is greatly reduced.

Description

technical field [0001] The invention belongs to the field of signal processing, and relates to a method for recovering noise-containing signals based on compression sensing iterations of threshold shrinkage. Background technique [0002] With the rapid development of information technology, people have higher and higher requirements for information acquisition and processing speed. Traditional sampling based on the Nyquist theorem requires the sampling speed to be at least twice the highest frequency of the signal to be tested to ensure that information is not lost, making it increasingly difficult to process high-frequency and broadband signals. Compressed sensing, which appeared in 2006, is completely different from traditional sampling. The sampling rate is determined by the information rate, that is, the amount of non-zero information. In just a few years, it has been applied to many engineering fields, such as radar imaging, face recognition, radar direction of arrival...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): H03M7/30
Inventor 胡辽林王斌薛瑞洋
Owner XIAN UNIV OF TECH
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com