Looking for breakthrough ideas for innovation challenges? Try Patsnap Eureka!

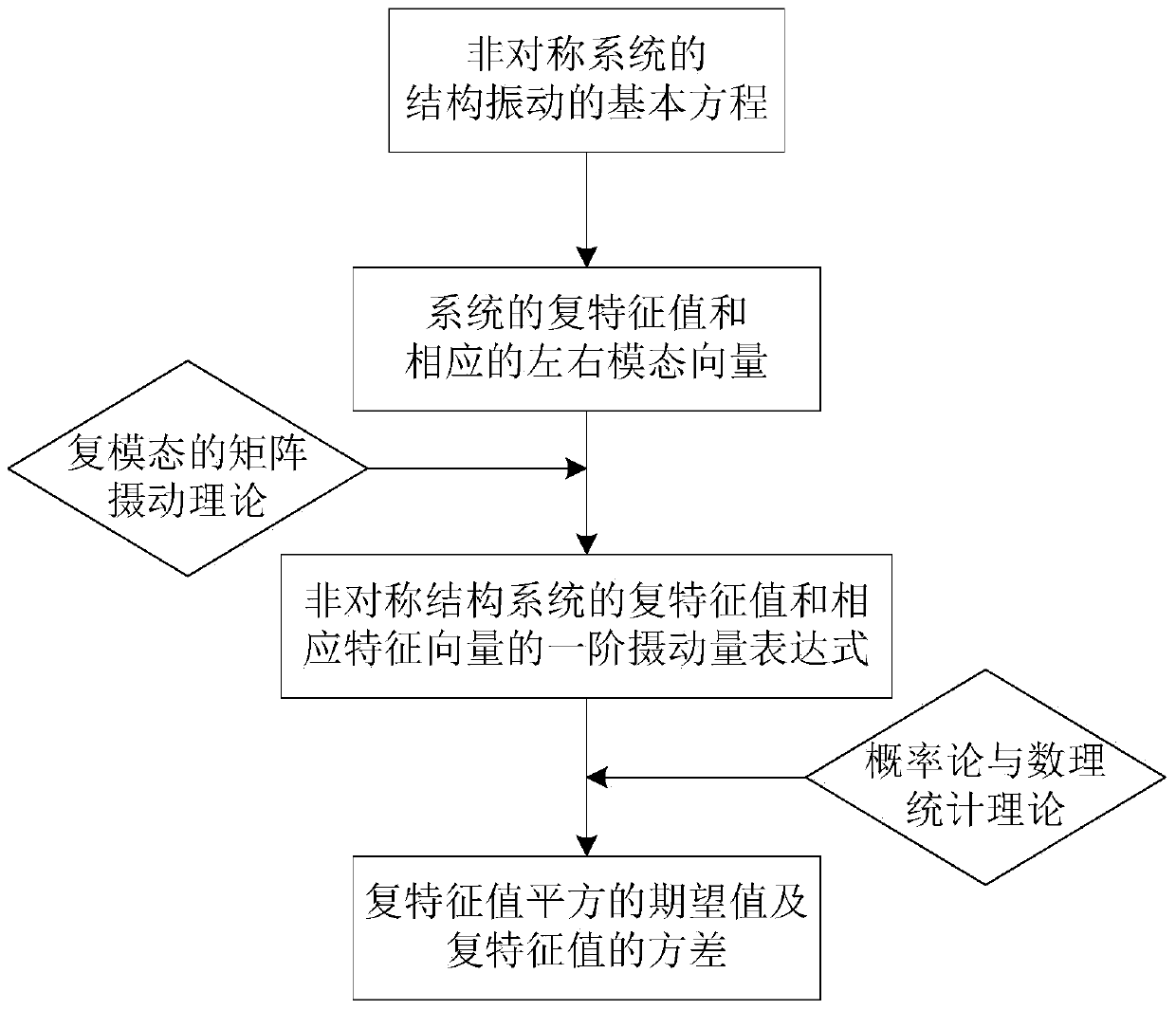
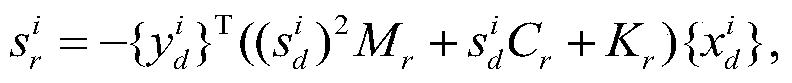A Direct Variance Calculation Method of Complex Mode Stochastic Eigenvalues ​​Based on Matrix Perturbation Theory

A technology of modal eigenvalues ​​and complex eigenvalues, applied in complex mathematical operations and other directions, can solve the problems of perturbation methods, structural complex eigenvalues ​​and their statistical properties, and other problems, and achieve a wide range of applications.

Inactive Publication Date: 2018-06-01
BEIHANG UNIV +2
View PDF4 Cites 0 Cited by
  • Summary
  • Abstract
  • Description
  • Claims
  • Application Information

AI Technical Summary

Problems solved by technology

[0004] At present, the research and application of matrix perturbation theory by scholars at home and abroad mostly focus on the structural real mode matrix perturbation method when the structural parameters of the system are real symmetric matrices, and in the perturbation method of structural complex mode theory, structural complex eigenvalue There is still little research on its statistical properties

Method used

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
View more

Image

Smart Image Click on the blue labels to locate them in the text.
Viewing Examples
Smart Image
  • A Direct Variance Calculation Method of Complex Mode Stochastic Eigenvalues ​​Based on Matrix Perturbation Theory
  • A Direct Variance Calculation Method of Complex Mode Stochastic Eigenvalues ​​Based on Matrix Perturbation Theory
  • A Direct Variance Calculation Method of Complex Mode Stochastic Eigenvalues ​​Based on Matrix Perturbation Theory

Examples

Experimental program
Comparison scheme
Effect test

Embodiment

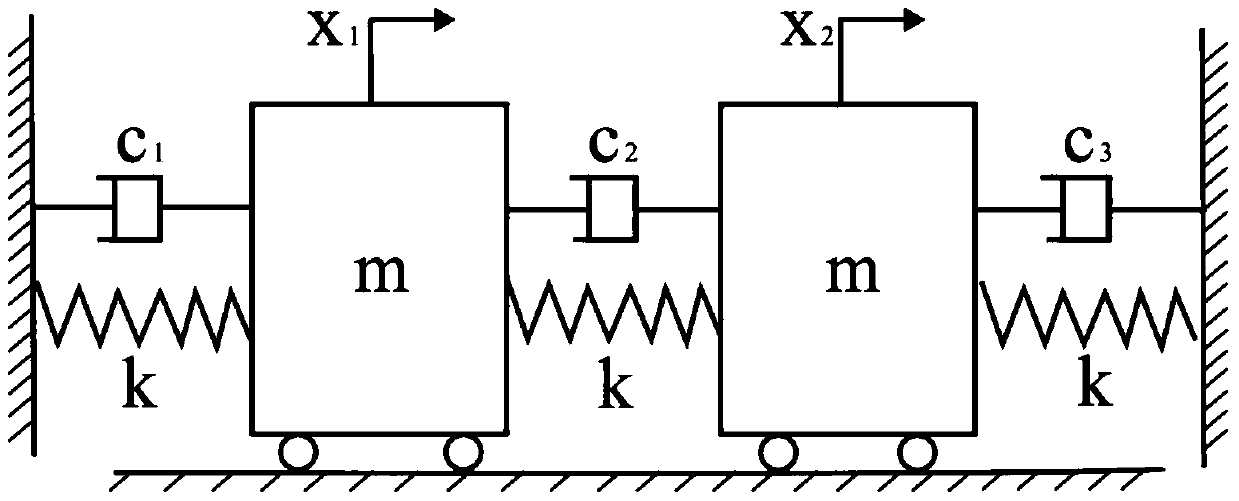
[0183] In order to understand more fully the characteristics of this invention and its applicability to engineering practice, the present invention uses figure 2 Taking the structural system as an example, the stochastic eigenvalue analysis of the complex mode is carried out. figure 2 middle c 1 ,c 2 ,c 3 Represent the damping coefficients of the three dampers in the system, k represents the stiffness coefficient of the spring in the system, m represents the mass of the slider, x 1 ,x 2 Respectively represent the position coordinates of the two sliders in the system.

[0184] Consider a two-degree-of-freedom vibration system that satisfies c=1, k=9, m=1, where the damping coefficient c 1 =c 2 =c 3 = c; use D'Alembert's principle to easily establish the differential equation of motion of the system:

[0185]

[0186] The state vector {u}, matrix A and matrix B of the system are:

[0187]

[0188] By the method in the above-mentioned invention, obtain easily:

...

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

PUM

No PUM Login to View More

Abstract

The invention discloses a complex mode random eigenvalue direct variance calculation method based on the matrix perturbation theory. According to the method, first, the complex mode eigenvalue of structure vibration and the first-order perturbation quantity of corresponding eigenvectors generated when the rigidity, the damping, the mass and other parameters of a structure are changed are derived according to the matrix perturbation theory; then, a direct variance calculation algorithm for calculating the change range of the structure complex mode eigenvalue is established based on the eigenvalue of the complex mode structure and the first-order perturbation quantity of the eigenvectors according to the probability theory. When complex eigenvalue analysis of an asymmetric structure system is performed, the change range of the complex mode eigenvalue of the structure system can be rapidly and accurately acquired without knowing or supposing correlation coefficient matrixes of structure parameters, and therefore engineering application of the method to large structures is greatly facilitated.

Description

technical field [0001] The present invention is applicable to the analysis of eigenvalues ​​of complex modal structural systems, and is used to solve the statistical properties and variation range of complex modal eigenvalues ​​of the structural systems under the condition of various disturbances. Modal eigenvalue analysis techniques provide guidance. Background technique [0002] As a practical tool for fast sensitivity analysis and fast structural reanalysis, the matrix perturbation method has received extensive attention in basic theory and engineering applications and has achieved considerable development. X.W.YANG and S.H.CHEN applied Pade approximation to matrix perturbation theory, and obtained the expressions of eigenvector and eigenvalue variation. Kaminski M and Solecka M expanded the structural eigenvalues ​​and eigenvectors with the method of chaotic polynomial (PCE), and studied the forced vibration response analysis of linear stochastic systems. Debraj G appl...

Claims

the structure of the environmentally friendly knitted fabric provided by the present invention; figure 2 Flow chart of the yarn wrapping machine for environmentally friendly knitted fabrics and storage devices; image 3 Is the parameter map of the yarn covering machine
Login to View More

Application Information

Patent Timeline
no application Login to View More
Patent Type & Authority Patents(China)
IPC IPC(8): G06F17/16
Inventor 邱志平仇翯辰王晓军王喜鹤王冲许孟辉李云龙何巍
Owner BEIHANG UNIV
Who we serve
  • R&D Engineer
  • R&D Manager
  • IP Professional
Why Patsnap Eureka
  • Industry Leading Data Capabilities
  • Powerful AI technology
  • Patent DNA Extraction
Social media
Patsnap Eureka Blog
Learn More
PatSnap group products

Browse by: Latest US Patents, China's latest patents, Technical Efficacy Thesaurus, Application Domain, Technology Topic, Popular Technical Reports.

© 2024 PatSnap. All rights reserved.Legal|Privacy policy|Modern Slavery Act Transparency Statement|Sitemap|About US| Contact US: help@patsnap.com