
What Is Conservation of Angular Momentum?
Angular momentum is a vector quantity that describes the amount of rotation an object has and the axis about which it rotates. It is a conserved quantity in a closed system, meaning that the total angular momentum remains constant unless an external torque acts on the system. The mathematical formulation for angular momentum (L) of a point particle is given by:
L = r × p
Where r is the position vector of the particle relative to the axis of rotation, and p is the linear momentum of the particle. For a rigid body rotating about a fixed axis, the angular momentum is expressed as:
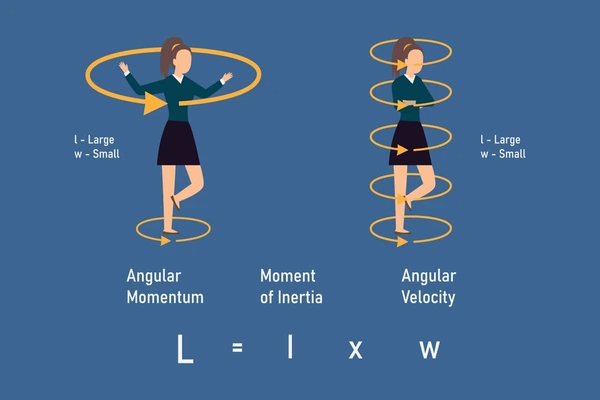
L = Iω
Where I is the moment of inertia of the body, and ω is the angular velocity.
Key Principles of Angular Momentum
Angular Momentum and Its Conservation
Angular momentum is a vector quantity that describes the amount of rotation an object has and the axis around which it rotates. The law of conservation of angular momentum states that the total angular momentum of an isolated system remains constant unless an external torque acts upon it. This principle arises from the rotational symmetry of space and is a fundamental law of physics.
Relation to Linear Momentum
Linear momentum is conserved because physical laws remain unchanged under spatial translations, reflecting the homogeneity of space. Angular momentum conservation arises due to rotational symmetry, meaning physical laws stay consistent under rotations in space. This principle directly connects to linear momentum conservation and highlights the symmetry of physical laws in rotational systems.
Mathematical Formulation
For a single particle, angular momentum L is defined as the cross product of the particle’s position vector r and its linear momentum p: L = r × p. For a system of particles, the total angular momentum is the vector sum of the angular momenta of all the particles. If no external torque acts on the system, the total angular momentum remains constant: dL/dt = 0.
Examples of Conservation of Angular Momentum
- Spinning Figure Skater: When a skater pulls their arms inward, their moment of inertia decreases, increasing their angular velocity to conserve angular momentum.
- Planetary Motion: A planet orbiting the Sun maintains constant angular momentum due to the lack of external torques, ensuring orbital stability.
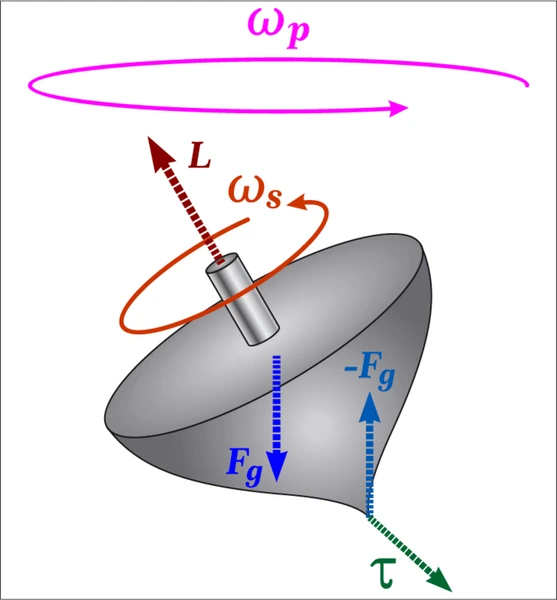
- Gyroscopic Precession: The angular momentum vector of a spinning gyroscope resists orientation changes. Under external torque, it precesses, moving perpendicularly to the applied force. This is essential in navigation and attitude control systems, ensuring stability in gyroscopes, spacecraft, and aircraft.
- Magnetic Bearings: Magnetic bearings leverage angular momentum conservation to levitate and rotate objects without contact, enabling frictionless motion and high-speed rotations.
Mathematical Explanation
The principle of conservation of angular momentum states that the total angular momentum of an isolated system remains constant unless an external torque acts upon it. Mathematically, it can be expressed as:
dL/dt = τ
Where L is the angular momentum vector, t is time, and τ is the net external torque acting on the system. If the net external torque is zero, then the angular momentum remains constant.
For a single particle of mass m moving with velocity v relative to a point O, the angular momentum is given by:
L = r × mv
Where r is the position vector of the particle relative to O.
For a rigid body rotating about a fixed axis with angular velocity ω, the angular momentum is:
L = Iω
Where I is the moment of inertia of the body about the axis of rotation.
Applications of Conservation of Angular Momentum
Rotational Motion and Stability
The conservation of angular momentum plays a crucial role in understanding and predicting the rotational behavior of objects. It governs the motion of spinning objects, such as tops, gyroscopes, and planetary bodies. This principle explains why a spinning figure skater can increase their rotational speed by pulling in their arms, reducing their moment of inertia. It also elucidates the stability of rotating systems, like a bicycle remaining upright due to the conservation of angular momentum.
Spacecraft and Satellite Maneuvers
It is essential in space exploration and satellite operations. Spacecraft use reaction wheels or control moment gyroscopes to adjust orientation or maintain attitude without using propellant. These systems rely on angular momentum conservation, allowing precise attitude adjustments through internal momentum transfer. This principle also governs the deployment and detachment of satellites from launch vehicles, ensuring accurate control over their rotational dynamics for stable and predictable positioning in space.
Astrophysical Phenomena
The conservation of angular momentum is fundamental in understanding the formation and evolution of celestial bodies. It explains the rotation of galaxies, stars, and planetary systems, as well as the accretion of matter onto black holes. This principle also governs the dynamics of binary star systems and the formation of accretion disks around compact objects.
Engineering Applications
It finds applications in various engineering fields. In mechanical engineering, it is utilized in the design of flywheels, turbines, and rotating machinery. In civil engineering, it is essential for understanding the behavior of structures under rotational loads, such as wind turbines and tall buildings. Additionally, it plays a role in the development of control systems for robotics and automation.

Latest Technical Innovations in Conservation of Angular Momentum
Theoretical and Computational Advances
- Formalism in partially coherent wave fields: Researchers have developed a general formalism using the Maxwell stress tensor to analyze angular momentum properties in partially coherent electromagnetic beams exhibiting circulation. This framework offers insights into the complex dynamics of angular momentum in such fields.
- Addressing violations of angular momentum conservation in ultrafast spin dynamics simulations: Recent studies highlight violations of angular momentum conservation in ultrafast spin dynamics simulations caused by oversimplified spin-orbit coupling models. Refining the spin-orbit coupling implementation restores conservation, enhancing the accuracy of real-time simulations.
Experimental Techniques and Setups
- Magnetic bearing apparatus for demonstrating it: A rugged and easy-to-use device derived from a magnetic levitation toy has been developed to experimentally verify angular momentum conservation.
- Backscattered polarization patterns: The occurrence of backscattered polarization patterns has been linked to the conservation of angular momentum, providing a model to account for helicity-maintaining and helicity-flipping scattering processes.
Novel Concepts and Designs
Inexpensive apparatus for studying: Low-cost prototypes and setups have been developed for educational purposes, allowing students to investigate collisions and rotational dynamics through the lens of angular momentum conservation.
The engine for self-propulsion of energy beam sources: A proposed system applies conservation of angular momentum to a laser beam emanating from a solid object, causing the beam to travel in a decreasing circular path and propelling the source.
FAQs
- What is angular momentum?
Angular momentum is the rotational equivalent of linear momentum, representing the product of rotational mass (moment of inertia) and angular velocity. - Why is conservation of angular momentum important?
It explains how rotational systems behave when no external torque is applied, allowing predictions in physics, engineering, and astronomy. - How does angular momentum apply to planetary motion?
Planets conserve angular momentum as they orbit stars, speeding up when closer and slowing down when farther away. - What is the difference between linear and angular momentum?
Linear momentum relates to straight-line motion, while angular momentum deals with rotational motion. - Can angular momentum change in a closed system?
No, in a closed system without external torques, angular momentum remains constant.
To get detailed scientific explanations of conservation of angular momentum, try Patsnap Eureka.

